某中学组建了A、B、C、D、E五个不同的社团组织，为培养学生的兴趣爱好，要求每个学生必须参加，且只能参加一个社团．假定某班级的甲、乙、丙三名学生对这五个社团的选择是等可能的．
(I)求甲、乙、丙三名学生参加五个社团的所有选法种数；
(Ⅱ)求甲、乙、丙三人中至少有两人参加同一社团的概率；
(Ⅲ)设随机变量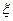
为甲、乙、丙这三个学生参加A社团的人数，求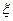的分布列与
数学期望．
相关试题
.
的定义域；
轴；
满足什么关系时，
在
上恒取正值.
是定义在R上的奇函数，当
时，
，其中
且
.
的值；（2）求
（其中
），且
的图像在
轴右侧的第一个最高点的横坐标为
.
的值；（2）如果
在区间
上的最小值为
，求
的值.
.
的周期和单调递增区间；
的图象经过怎样变化得到.
的值．
，
,
，求
的值．相关知识点
推荐套卷
某中学组建了A、B、C、D、E五个不同的社团组织，为培养学生的兴趣爱好，要求每个学生必须参加，且只能参加一个社团．假定某班级的甲、乙、丙三名学生对这五个社团的选择是等可能的．
(I)求甲、乙、丙三名学生参加五个社团的所有选法种数；
(Ⅱ)求甲、乙、丙三人中至少有两人参加同一社团的概率；
(Ⅲ)设随机变量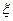为甲、乙、丙这三个学生参加A社团的人数，求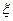的分布列与
数学期望．
粤公网安备 44130202000953号