有下列命题:
①在函数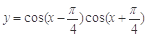 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为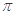 ;
;
②命题:“若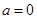 ,则
,则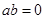 ”的否命题是“若
”的否命题是“若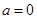 ,则
,则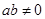 ”;
”;
③“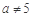 且
且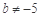 ”是“
”是“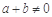 ”的必要不充分条件;
”的必要不充分条件;
④已知命题p:对任意的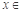 R,都有
R,都有 ,则
,则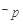 是:存在
是:存在 ,使得
,使得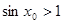 ;
;
⑤命题“若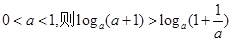 ”是真命题;
”是真命题;
⑥在△ABC中,若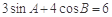 ,
,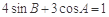 ,则角C等于
,则角C等于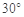 或
或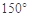 .
.
其中所有真命题的序号是 .
已知函数 的图象与
的图象与 轴交点的横坐标构成一个公差为
轴交点的横坐标构成一个公差为 的等差数列,把函数
的等差数列,把函数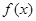 的图象沿
的图象沿 轴向右平移
轴向右平移 个单位,得到函数
个单位,得到函数 的图象.若在区间
的图象.若在区间 上随机取一个数
上随机取一个数 ,则事件“
,则事件“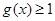 ”发生的概率为
”发生的概率为
A. |
B.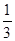 |
C. |
D.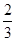 |
关于函数 ,看下面四个结论:
,看下面四个结论:
① 是奇函数;
是奇函数;
②当 时,
时, 恒成立;
恒成立;
③ 的最大值是
的最大值是 ;
;
④ 的最小值是
的最小值是 .
.
其中正确结论的个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设函数
 的最小正周期为
的最小正周期为 ,
, 是函数
是函数 图象的一个对称中心,且曲线
图象的一个对称中心,且曲线 在该点处切线的斜率为
在该点处切线的斜率为 .
.
(1)求a,b, 的值;
的值;
(2)若角 的终边不共线,且
的终边不共线,且 ,求
,求 的值;
的值;
(3)若函数 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,判断:曲线
对称,判断:曲线 上是否存在与直线
上是否存在与直线 (c为常数)垂直的切线?证明你的结论.
(c为常数)垂直的切线?证明你的结论.
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)将 的图象向左平移
的图象向左平移 个单位长度,再将得到的图象横坐标变为原来的2倍(纵坐标不变),得到
个单位长度,再将得到的图象横坐标变为原来的2倍(纵坐标不变),得到 的图象;若函数
的图象;若函数 在区间
在区间 上的图象与直线
上的图象与直线 有三个交点,求实数a的取值范围.
有三个交点,求实数a的取值范围.
已知向量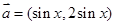 ,
,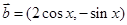 ,函数
,函数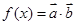 .
.
(1)求函数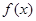 的最小正周期;
的最小正周期;
(2)求函数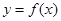 在
在 上的值域.
上的值域.