设函数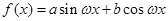
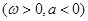的最小正周期为
，
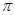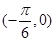是函数
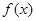图象的一个对称中心，且曲线
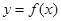在该点处切线的斜率为
．
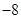（1）求a，b，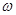
的值；
（2）若角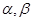
的终边不共线，且
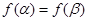，求
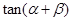的值；
（3）若函数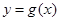
的图象与函数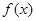的图象关于直线
对称，判断：曲线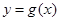上是否存在与直线
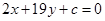（c为常数）垂直的切线？证明你的结论．
相关试题
的值；
的最大值和最小值
为等差数列，且
，
。
满足
，
，求
的定义域为A，g(x)=lg［(x－a－1)(2a－x)］(a＜1)的定义域为B.
A，求实数a的取值范围.
的值.
相关知识点
推荐套卷
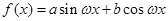
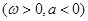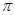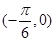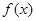设函数的最小正周期为，是函数图象的一个对称中心，且曲线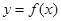在该点处切线的斜率为．
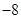（1）求a，b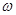，的值；
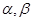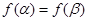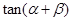（2）若角的终边不共线，且，求的值；
（3）若函数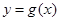的图象与函数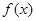的图象关于直线对称，判断：曲线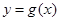上是否存在与直线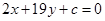（c为常数）垂直的切线？证明你的结论．
粤公网安备 44130202000953号