（本题10分）
已知函数f(x)=x3+ax2+bx+c（x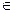
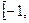
）在x=1和x=－
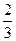处都取得极值。
（1） 求a、b的值；
（2） 求函数f(x)的单调递增区间；
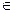
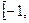
（3） 若对任意x，f(x)<c2恒成立，求实数c的取值范围。
相关试题
的顶点在坐标原点
，对称轴为
轴，焦点为
,抛物线上一点
的横坐标为2，且
.
作直线
交抛物线于
，
.
的椭圆
一个焦点为
.
的方程；
交椭圆
两点,且
，求直线
.
的单调区间；
，求函数
解集为
,不等式
解集为
，不等式
解集为
.
；
的取值范围.
为
，
的等差中项.
，求b，c的值.推荐套卷
（本题10分）
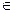
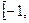
已知函数f(x)=x3+ax2+bx+c（x）在x=1和x=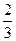－处都取得极值。
（1） 求a、b的值；
（2） 求函数f(x)的单调递增区间；
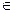
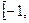
（3） 若对任意x，f(x)<c2恒成立，求实数c的取值范围。
粤公网安备 44130202000953号