高中数学多面角及多面角的性质解答题

（本小题满分12分）f（x）=．，其中向量=（m，cos2x），=（1+sin2x，1），，且函数 的图象经过点．
（Ⅰ）求实数的值．
（Ⅱ）求函数的最小值及此时值的集合。

（本题10分） 已知:函数 
（Ⅰ）求的值；   
（Ⅱ）设∈（0，），f（）＝－，求sin的值．

（本小题满分12分）
已知函数的最小正周期为．
（Ⅰ）求的值及函数的单调递增区间；
（Ⅱ）当时，求函数的取值范围．

（ 12分）已知函数，x∈R．
（1）求证的最小正周期和最值；
（2）求这个函数的单调递增区间．

（本小题满分12分）设向量 
（Ⅰ）若与垂直，求的值；
（Ⅱ）求的最大值．

（本题12分）已知向量，，其中．设函数．
（1）求函数的最小正周期；
（2）求函数在上的最大值和最小值．

已知函数（ω＞0）的最小正周期为π．
（Ⅰ）求ω的值及函数f（x）的单调递增区间；
（Ⅱ）当时，求函数f（x）的取值范围．

求函数在区间[0,]上的最值

（本小题满分10分）设△的三边为满足．
（1）求的值；
（2）求的取值范围．

设函数
（Ⅰ）当，求函数的单调区间与极值；
（Ⅱ）若函数在上是增函数，求实数的取值范围．

已知向量，且函数在时取得最小值．
（Ⅰ）求的值；
（Ⅱ）在中，分别是内角的对边，若，，，求的值．

已知函数（）的周期为.
（1）当时，求函数的值域；
（2）已知的内角，，对应的边分别为，，，若，且，，求的面积.

已知函数（），其中，，满足以下两个条件：①两条相邻对称轴之间的距离为；②．
（Ⅰ）求函数的解析式；
（Ⅱ）求函数在内的单调递增区间；
（Ⅲ）若方程在内有个不等实根，求实数的取值范围．

（本题12分）已知,,．
（1）求的单调递减区间;
（2）若函数，求当时,的最大值．

（本小题满分12分）
已知函数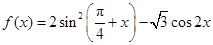
（1）求函数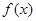的最大值，以及取到最大值时所对应的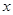的集合；
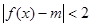（2）在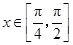上恒成立，求实数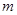的取值范围。