高中数学多面角及多面角的性质解答题

设向量a =, b =（其中实数不同时为零），当时，有a⊥b；当时，有a∥b.
（Ⅰ）求函数解析式；
（Ⅱ）设，且，求.

已知向量， 
（1）  求在上的单调增区间；
（2）  若，求 的值

（本小题满分12分）
已知函数
（Ⅰ）求的最小正周期和单调递增区间；
（Ⅱ）求在区间上的最大值和最小值．

本小题满分12分）
已知函数
（1）求函数的最小正周期及函数取最小值时自变量的集合
（2）确定函数的单调递增区间
（3）若函数y=sin2x的图象向右平移m个单位(|m|<)，向上平移n个单位后得到函数y=f(x)的图象，求实数m、n的值

已知f(x)=2cos²x+sin2x+a (a∈R , a为常数)
(Ⅰ) 若x∈R , 求f(x)的单调增区间; 
(Ⅱ) 若x∈[0, ]时, f(x)的最大值为4, 并求此时f(x)的最小值。

（本小题分14分）已知函数
（Ⅰ）求的最小正周期T；
（Ⅱ）求的最大值和最小值；
（Ⅲ）求当取最大值时值的集合。

已知函数，
（1）  求函数的定义域及值域；
（2）  判断该函数的奇偶性，并证明你的结论.

（本小题满分12分）
已知函数=sin(2x+)+sin(2x-)+cos2x+1(xÎR)．
(1)化简并求的最小正周期；
(2)求函数的最大值及此时自变量x的取值集合；
(3)求使≥2的x的取值范围．

（本小题满分14分）
已知函数+1，求：
（1）求函数的单调减区间；
（2）求函数的最大值，以及函数取得最大值时自变量的集合

（本小题满分14分）已知函数．
(1)求的单调递增区间； (2)求在区间上的最值及相应的x值．
（3）将函数的图象向左平移个单位后，所得的函数恰好是偶函数，求的最小值。

(本小题满分12分)
设函数f(x)=cos(2x+)+sinx.
（1）求函数f(x)的最小值及取得最小值时x的值。
（2）设A,B,C为ABC的三个内角，若cosB=，，且C为锐角，求sinA.

(本小题满分10分)
已知函数f (x)=a+bsinx+2cosx(x∈R)的图象经过点A(0,1),B.
(1)求函数f (x)的单调递减区间；
(2)由函数y=f (x)的图象经过平移是否能得到一个奇函数y=g(x)的图象？若能，请写出平移过程；若不能，请说明理由.

（本小题满分12分）
已知向量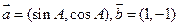,且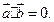
(Ⅰ)求tanA的值；
(Ⅱ)求函数R)的值域.

（本小题满分12分）
已知函数的最大值为3， 的图像的相邻两对称轴间的距离为2，在y轴上的截距为2.
（Ⅰ）求函数的解析式；
（Ⅱ）若m=,求f(m)+f(m+1)的值．

（本小题满分13分）已知（为常数）的图象关于原点对称，且.
（1）求的解析式；
（2）求的单调增区间.