高中数学多面角及多面角的性质选择题

已知函数的部分图象如图所示，则
函数的解析式为                                                 （   ）

A．

B．

C．

D．

已知函数则是  （   ）

A．单调递增函数	B．单调递减函数
C．奇函数	D．偶函数

已知函数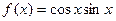，给出下列四个说法：
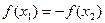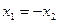①若，则；  ②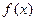的最小正周期是2π；
③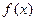在区间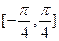上是增函数； ④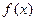的图象关于直线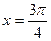对称．
其中正确说法的个数为                                               （   ）

A．1

B．2

C．3

D．4

如图，四位同学在同一个坐标系中分别选定了一个适当的区间，各自作出三个函数 $y=2\sin 2x$ ， $y=\sin \left(x+\frac{\pi }{6}\right)$ ， $y=\sin \left(x-\frac{\pi }{3}\right)$ 的图像如下。结果发现其中有一位同学作出的图像有错误，那么有错误的图像是（  ）

A．
B．
C．
D．

函数 $y={\sin }^{2}x+\sin x-1$的值域为（）

A．

$\left[-1,1\right]$

B．

$\left[-\frac{5}{4},-1\right]$

C．

$\left[-\frac{5}{4},1\right]$

D．

$\left[-1,\frac{5}{4}\right]$

函数 $f\left(x\right)=\sqrt{3}\sin (\frac{x}{2}-\frac{\pi }{4}),x\in R$的最小正周期为（   ）.

A．

$\frac{\pi }{2}$

B．

$x$

C．

$2\pi$

D．

$4\pi$

.已知函数f(x) = 2sinωx + 1在[0,]上单调递增，且在这个区间上的最大值为,则实数ω的一个可能值是(   )   

A．

B．

C．或

D．

已知函数 $y=\sin (\omega x+\phi )(\omega >0,\left|\phi \right|<\frac{\pi }{2})$ 的部分图象如图所示，则（  ）

A．	$\omega =1,\phi =\frac{\pi }{6}$	B．	$\omega =1,\phi =-\frac{\pi }{6}$
C．	$\omega =2,\phi =\frac{\pi }{6}$	D．	$\omega =2,\phi =-\frac{\pi }{6}$

下列函数中，周期为 $\pi$，且在 $\left[\frac{\pi }{4},\frac{\pi }{2}\right]$上为减函数的是（）

A．	$y=\sin \left(2x+\frac{\pi }{2}\right)$	B．	$y=\cos \left(2x+\frac{\pi }{2}\right)$
C．	$y=\sin \left(x+\frac{\pi }{2}\right)$	D．	$y=\cos \left(x+\frac{\pi }{2}\right)$

为了得到函数的图像，只需把函数的图像（）

A．	向左平移 个长度单位	B．	向右平移 个长度单位
C．	向左平移 个长度单位	D．	向右平移 个长度单位

为了得到这个函数的图象，只要将的图象上所有的点

A．向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变

B．向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变

C．向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变

D．向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变

设 $\omega >0$,函数 $y=\sin \left(\omega x+\frac{\pi }{3}\right)+2$的图像向右平移 $\frac{4\pi }{3}$个单位后与原图像重合，则 $\omega$的最小值是（）

A．

$\frac{2}{3}$

B．

$\frac{4}{3}$

C．

$\frac{3}{2}$

D．

$3$

给出下列三个命题：
①函数 $y=\frac{1}{2}\ln \frac{1-\cos x}{1+\cos x}$ 与 $y=\mathrm{lnt}an\frac{x}{2}$ 是同一函数；
②若函数 $y=f\left(x\right)$ 与 $y=g\left(x\right)$ 的图像关于直线 $y=x$ 对称，则函数 $y=f\left(2x\right)$ 与 $y=\frac{1}{2}g\left(x\right)$ 的图像也关于直线 $y=x$ 对称；

③若奇函数 $f\left(x\right)$ 对定义域内任意 $x$ 都有 $f\left(x\right)=f\left(2-x\right)$ ,则 $f\left(x\right)$ 为周期函数．
其中真命题是（  ）

A．

①②

B．

①③

C．

②③

D．

②

设 $\omega >0$,函数 $y=\sin (\omega x+\frac{\pi }{3})+2$的图像向右平移 $\frac{4\pi }{3}$个单位后与原图像重合，则 $\omega$的最小值是

A．

$\frac{2}{3}$

B．

$\frac{4}{3}$

C．

$\frac{3}{2}$

D．

$3$

设函数 $f\left(x\right)=4\sin (2x+1)-x$，则在下列区间中函数 $f\left(x\right)$不存在零点的是

A．

$[-4,-2]$

B．

$[-2,0]$

C．

$[0,2]$

D．

$[2,4]$