2010年全国统一高考理科数学试卷(浙江卷)
设,则""是""的()
| A. | 充分而不必要条件 | B. | 必要而不充分条件 |
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
设
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
| A. | 若 ,则 | B. | 若 ,则 |
| C. | 若 ,则 | D. | 若 ,则 |
设分别为双曲线的左、右焦点.若在双曲线右支上存在点,满足,且到直线的距离等于双曲线的实轴长,则该双曲线的渐近线方程为()
| A. | B. | C. | D. |
设函数的集合,平面上点的集合,则在同一直角坐标系中,中函数的图象恰好经过中两个点的函数的个数是()
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
有4位同学在同一天的上、下午参加"身高与体重"、"立定跳远"、"肺活量"、"握力"、"台阶"五个项目的测试,每位同学上、下午各测试一个项目,且不重复. 若上午不测"握力"项目,下午不测"台阶"项目,其余项目上、下午都各测试一人. 则不同的安排方式共有 种(用数字作答).
如图,一个小球从 处投入,通过管道自上而下落 或 或 。已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到 , , ,则分别设为l,2,3等奖.

(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量
为获得
(
)等奖的折扣率,求随机变量
的分布列及期望
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量
为获得1等奖或2等奖的人次,求
.
如图,在矩形 中,点 分别在线段 上, .沿直线 将 翻折成 ,使平面 .
(Ⅰ)求二面角
的余弦值;
(Ⅱ)点
分别在线段
上,若沿直线
将四边形
向上翻折,使
与
重合,求线段
的长.

已知
,直线
,椭圆
,
分别为椭圆
的左、右焦点.
(Ⅰ)当直线
过右焦点
时,求直线
的方程;
(Ⅱ)设直线
与椭圆
交于
两点,
,
的重心分别为
.若原点
在以线段
为直径的圆内,求实数
的取值范围.

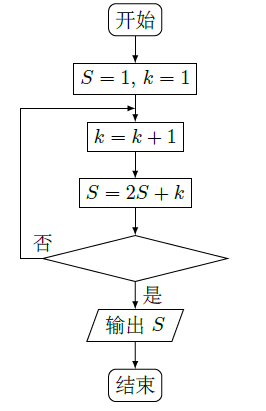
 项和,,则()
项和,,则()


 粤公网安备 44130202000953号
粤公网安备 44130202000953号