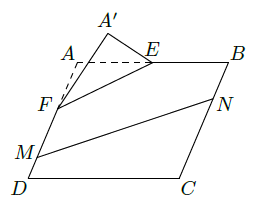
如图,在矩形 中,点 分别在线段 上, .沿直线 将 翻折成 ,使平面 .
(Ⅰ)求二面角
的余弦值;
(Ⅱ)点
分别在线段
上,若沿直线
将四边形
向上翻折,使
与
重合,求线段
的长.
推荐套卷
如图,在矩形 中,点 分别在线段 上, .沿直线 将 翻折成 ,使平面 .
(Ⅰ)求二面角
的余弦值;
(Ⅱ)点
分别在线段
上,若沿直线
将四边形
向上翻折,使
与
重合,求线段
的长.
