已知
,直线
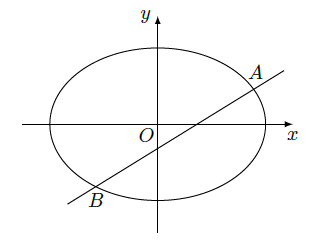
,椭圆
,
分别为椭圆
的左、右焦点.
(Ⅰ)当直线
过右焦点
时,求直线
的方程;
(Ⅱ)设直线
与椭圆
交于
两点,
,
的重心分别为
.若原点
在以线段
为直径的圆内,求实数
的取值范围.
推荐套卷
已知
,直线
,椭圆
,
分别为椭圆
的左、右焦点.
(Ⅰ)当直线
过右焦点
时,求直线
的方程;
(Ⅱ)设直线
与椭圆
交于
两点,
,
的重心分别为
.若原点
在以线段
为直径的圆内,求实数
的取值范围.
