高中数学多面角及多面角的性质试题

函数f(x)＝A·tan(ωx+φ)(φ＞0)在区间[m，n]上的函数值都小于0，则函数g(x)＝A·cot(ωx+φ)在[m，n]上的函数值

A．都大于0，且有最大值为g(m)	B．都小于0，且有最大值为g(m)
C．都大于0，且有最小值为g(m)	D．都小于0，且有最小值为g(m)

设，下列命题：①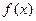既不是奇函数，又不是偶函数；②若是三角形内角，则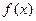是增函数；③若是三角形内角，则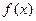有最大值，无最小值； ④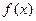的最小正周期为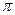，其中正确命题的序号是    (    )

A．①②

B．①③

C．②③

D．②④

（本小题满分12分）函数的图像上相邻的最高点与最低点的坐标分别为和 。 （1）求出的解析式。（2）找出图像的对称中心和的递增区间。

（本小题满分14分）已知函数．(1) 求函数的最小正周期，并写出函数图象的对称轴方程；(2) 若，求函数的值域．

（本小题满分14分）已知函数（其中A>0，）的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为.（Ⅰ）求的解析式；（Ⅱ）当，求的值域；

（本小题满分14分）已知函数是的导函数。
（Ⅰ）求函数的最大值和最小正周期；
（Ⅱ）若的值。

(本小题满分13分)已知函数．(Ⅰ)当时，求的最小正周期和值域；(Ⅱ)若函数在区间上是增函数，求实数的取值范围．

函数（其中，）的图象如图所示，若点A是函数的图象与x轴的交点，点B、D分别是函数的图象的最高点和最低点，点C是点B在x轴上的射影，则=       。

已知函数 （I）求函数的最小正周期；（II）求函数的单调增区间。

设函数f (x)=2cosx (cosx+sinx)－1,x∈R(1)求f (x)的最小正周期T；(2)求f (x)的单调递增区间.

设函数给出下列四个论断：
① 它的周期为；
② 它的图象关于直线对称；
③它的图象关于点对称；④在区间上是增函数。 
请以其中两个论断为条件，另两个为结论，写出一个正确的命题：                                           .（用符号表示）

(12分)已知，，且，求：
⑴·及；
⑵若的最小值为－，求实数的值.

关于的方程一定有实数解，则的取值范围是___　　_______.

已知函数，（1）求的值；（2）若，求的值域.

设函数，则下列结论正确的是                   （   ）

A．的图像关于直线对称	B．的图像关于点对称
C．把的图像向左平移个单位，得到一个偶函数的图像
D．的最小正周期为，且在上为增函数