设函数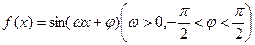
给出下列四个论断：
① 它的周期为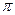
；
② 它的图象关于直线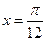
对称；
③它的图象关于点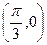
对称；④在区间
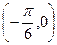上是增函数。
请以其中两个论断为条件，另两个为结论，写出一个正确的命题： .（用符号表示）
相关试题
，当
时，函数
有极值为
，
有3个解，求实数
的取值范围。
．
的最小正周期；
为一次函数，
，且满足
有零点，求
的取值范围.
的公差为
,且
,数列
的前
项和为
,且
=
求证：数列
的前
。
，cosC是方程
的一个根，求△ABC周长的最小值。相关知识点
推荐套卷
设函数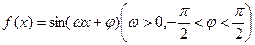给出下列四个论断：
① 它的周期为；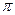
② 它的图象关于直线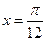对称；
③它的图象关于点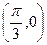对称；④在区间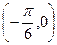上是增函数。
请以其中两个论断为条件，另两个为结论，写出一个正确的命题： .（用符号表示）
粤公网安备 44130202000953号