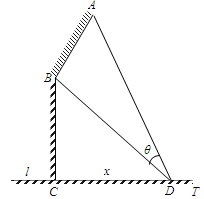
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60o(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4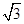 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.
在△ABC中,角A,B,C所对边的边长分别是a,b,c.
(1)若c=2,C=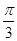 且△ABC的面积等于
且△ABC的面积等于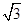 ,求cos(A+B)和a,b的值;
,求cos(A+B)和a,b的值;
(2)若B是钝角,且cos A=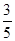 ,sin B=
,sin B=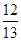 ,求sin C的值.
,求sin C的值.
在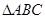 中,角
中,角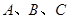 所对的边为
所对的边为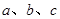 ,且满足
,且满足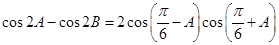
(1)求角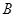 的值;
的值;
(2)若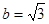 且
且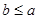 ,求
,求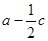 的取值范围.
的取值范围.
已知函数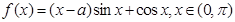 .
.
(1)当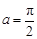 时,求函数
时,求函数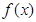 值域;
值域;
(2)当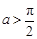 时,求函数
时,求函数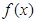 的单调区间.
的单调区间.
(本小题12分)已知 满足
满足 .
.
(1)将 表示为
表示为 的函数
的函数 ,并求
,并求 的单调递增区间;
的单调递增区间;
(2)已知 三个内角
三个内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若 ,且
,且 ,求
,求 面积的最大值.
面积的最大值.
(本小题满分12分)如下图所示,某海轮以 海里/小时的速度航行,在
海里/小时的速度航行,在 点测得海面上油井
点测得海面上油井 在南偏东
在南偏东 ,向北航行
,向北航行
 分钟后到达
分钟后到达 点,测得油井
点,测得油井 在南偏东
在南偏东 ,海轮改为北偏东
,海轮改为北偏东 的航向再行驶
的航向再行驶 分钟到达
分钟到达 点,求
点,求 间的距离.
间的距离.
(本小题满分14分)
在DABC中,角A、B、C所对的边分别为a、b、c,若 ,
,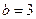 ,
, .
.
(I) 求c的值; (II) 求 的值.
的值.
(本小题满分12分)在平面直角坐标系中,已知
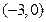 ,
,
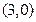 ,
, (
( ),
),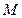
 ,O为坐标原点,若实数
,O为坐标原点,若实数 使向量
使向量 ,
, 和
和 满足:
满足: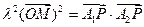 ,设点P的轨迹为
,设点P的轨迹为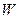 .
.
(Ⅰ)求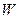 的方程,并判断
的方程,并判断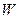 是怎样的曲线;
是怎样的曲线;
(Ⅱ)当 时,过点
时,过点 且斜率为1的直线与
且斜率为1的直线与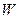 相交的另一个交点为
相交的另一个交点为 ,能否在直线
,能否在直线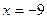 上找到一点
上找到一点 ,恰使
,恰使 为正三角形?请说明理由.
为正三角形?请说明理由.