在△ABC中,设AD为BC边上的高,且AD = BC,b,c分别表示角B,C所对的边长,则 的取值范围是_______ .
的取值范围是_______ .
在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、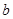 、
、 ,
,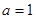 ,
, ,当
,当 的面积等于
的面积等于 时,
时, _______________.
_______________.
有下列六个命题:
(1)一定存在直线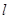 ,使函数
,使函数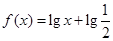 的图像与函数
的图像与函数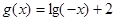 的图像关于直线
的图像关于直线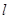 对称;
对称;
(2)直线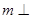 平面
平面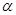 ,直线
,直线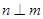 ,则
,则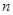 ∥
∥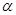 ;
;
(3)已知数列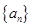 的前
的前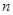 项和为
项和为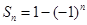 ,
,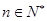 ,则数列
,则数列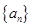 一定是等比数列;
一定是等比数列;
(4)过抛物线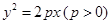 上的任意一点
上的任意一点 的切线方程一定可以表示为
的切线方程一定可以表示为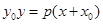 ;
;
(5)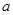 是正数,则“
是正数,则“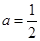 ”是“对任意正数
”是“对任意正数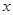 ,
,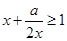 ”的充要条件;
”的充要条件;
(6)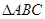 中,
中, ,则
,则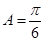 .则正确命题的个数是_______.
.则正确命题的个数是_______.
给出下列五个命题:
① 中,
中, 是
是 成立的充要条件;
成立的充要条件;
②当 时,有
时,有 ;
;
③已知 是等差数列
是等差数列 的前n项和,若
的前n项和,若 ,则
,则 ;
;
④若函数 为R上的奇函数,则函数
为R上的奇函数,则函数 的图象一定关于点
的图象一定关于点 成中心对称.
成中心对称.
⑤函数 有最大值为
有最大值为 ,有最小值为0。
,有最小值为0。
其中所有正确命题的序号为 .
在 中,若AC =" I," AB=
中,若AC =" I," AB= ,,
,,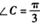 则BC =_________.
则BC =_________.
如右图,测量河对岸的塔高 时,可以选与塔底
时,可以选与塔底 在同一水平面内的两个测点
在同一水平面内的两个测点 与
与 ,测得
,测得 .
. ,
, 米,并在点
米,并在点 测得塔顶
测得塔顶 的仰角为
的仰角为 ,则塔高
,则塔高 =_________米.
=_________米.
(1)由“若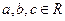 则
则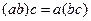 ”类比“若
”类比“若 为三个向量,则
为三个向量,则 ”;
”;
(2)在数列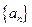 中,
中, ,猜想
,猜想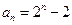 ;
;
(3)在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;
(4)若 则
则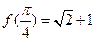 。
。
上述四个推理中,得出的结论正确的是__ _ _ 。(写出所有正确结论的序号)
某港口水的深度 (米)是时间
(米)是时间 (
( ,单位:时)的函数,记作
,单位:时)的函数,记作 , 下面是某日水深的数据:
, 下面是某日水深的数据:
| t/h |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
| y/m |
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经常期观察, 的曲线可以近似的看成函数
的曲线可以近似的看成函数 的图象,根据以上的数据,可得函数
的图象,根据以上的数据,可得函数 的近似表达式为 .
的近似表达式为 .