广东省高考猜押题卷文科数学(一)解析版
命题“若 是正弦函数,则
是正弦函数,则 是周期函数”的逆命题是( )
是周期函数”的逆命题是( )
A.若 是正弦函数,则 是正弦函数,则 不是周期函数 不是周期函数 |
B.若 是周期函数,则 是周期函数,则 是正弦函数 是正弦函数 |
C.若 不是正弦函数,则 不是正弦函数,则 不是周期函数 不是周期函数 |
D.若 不是周期函数,则 不是周期函数,则 不是正弦函数 不是正弦函数 |
在数学考试中,小明的成绩在90分以上的概率为0.18,在80~89分的概率为0.51,则小明在数学考试中成绩小于80分的概率为( ).
A. |
B. |
C. |
D. |
某种动物繁殖量 (只)与时间
(只)与时间 (年)的关系为
(年)的关系为 ,设这种动物第1年有100只,到第7年它们发展到 ( )
,设这种动物第1年有100只,到第7年它们发展到 ( )
| A.300只 | B.400只 | C.500只 | D.600只 |
如图1,已知E、F、G、H分别是正方体 的棱
的棱 、
、 、
、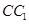 、
、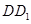 的中点,平面EFGH将正方体截去一个三棱柱后,得到图2所示的几何体,则此几何体的正视图和侧视图是( )
的中点,平面EFGH将正方体截去一个三棱柱后,得到图2所示的几何体,则此几何体的正视图和侧视图是( )
已知函数 ,x∈R,则
,x∈R,则 是( )
是( )
A.最小正周期为 的奇函数 的奇函数 |
B.最小正周期为 的偶函数 的偶函数 |
C.最小正周期为 的奇函数 的奇函数 |
D.最小正周期为 的偶函数 的偶函数 |
某调查机构就某单位职工的月收入调查了100人,并根据所得数据画了样本
的频率分布直方图(如图3).图4的程序框图是根据这100人中月收入在[2500,3000)
(元)的人数而设计的.那么框图中的判断框的①处应该填入的内容是 ?
选做题(14、15题,考生只能从中选做一题)
(几何证明选讲选做题)如图4,△ABC中,D、E分别在边AB、AC上,CD平分∠ACB,DE∥BC,如果AC=10,AE=4,那么BC=___________.
(本小题满分14分)
在DABC中,角A、B、C所对的边分别为a、b、c,若 ,
,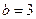 ,
, .
.
(I) 求c的值; (II) 求 的值.
的值.
(本小题满分12分)
某单位组织50名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,创导文明新风;2、到指定的社区、车站、码头做义工,帮助那些需要帮助的人。各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
| |
宣传慰问 |
义工救助 |
总计 |
| 20至40岁 |
11 |
16 |
27 |
| 大于40岁 |
15 |
8 |
23 |
| 总计 |
26 |
24 |
50 |
(Ⅰ) 用分层抽样方法在做义工的志愿者中随机抽取6名,大于40岁的应该抽取几名?
(Ⅱ) 在上述抽取的6名志愿者中任取2名,求恰有1名志愿者年龄大于40岁的概率.
(Ⅲ)如果“宣传慰问”与“做义工”是两个分类变量,并且计算出随机变量 ,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?
,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?
(本小题满分14分)
如图6,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,EF⊥PB交PB于点F.
(Ⅰ) 若PD=DC=2求三棱锥A-BDE的体积;
(Ⅱ) 证明PA∥平面EDB;
(Ⅲ) 证明PB⊥平面EFD.
已知椭圆G的中心在坐标原点,与双曲线 有相同的焦点,且过点
有相同的焦点,且过点 .
.
(Ⅰ) 求椭圆G的方程;
(Ⅱ) 设 、
、 是椭圆G的左焦点和右焦点,过
是椭圆G的左焦点和右焦点,过 的直线
的直线 与椭圆G相交于A、B两点,请问
与椭圆G相交于A、B两点,请问 的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线
的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
(本小题满分14分)
已知等差数列 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a, ,且
,且 .
.
(Ⅰ) a的值;
(Ⅱ) 若对于任意 ,总存在
,总存在 ,使
,使 ,求b的值;
,求b的值;
(Ⅲ) 在(Ⅱ)中,记 是所有
是所有 中满足
中满足 ,
, 的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记 为
为 的前n项和,
的前n项和, 是
是 的前n项和,求证:
的前n项和,求证: ≥
≥
 .
.
 ,
, },则
},则 ( )
( )



 满足
满足 ,则复数
,则复数 ( )
( )



 ,
,  ,如果向量
,如果向量 与
与 垂直,则
垂直,则 的值为 ( )
的值为 ( )


 、
、 满足约束条件:
满足约束条件: 则
则 的最优解为( )
的最优解为( )


 是
是 上的偶函数,
上的偶函数, . 当
. 当 时有
时有 ,则
,则 等于
等于



 和圆心为C的圆
和圆心为C的圆 相交于A、B两点,则线段AB的长度等于
相交于A、B两点,则线段AB的长度等于  ”是一种运算,对于任意的
”是一种运算,对于任意的 都满足
都满足 ,其中
,其中 为正实数,
为正实数, ,则
,则 取最大值时
取最大值时 的值为
的值为  (t为参数)与直线
(t为参数)与直线 平行,则常数
平行,则常数 = .
= . ,且不等式
,且不等式 的解集为
的解集为 。
。 有两个相等的实根,求
有两个相等的实根,求 的解析式;
的解析式; ,求实数
,求实数 的取值范围。
的取值范围。 (
( )存在零点,并求出零点.
)存在零点,并求出零点. 粤公网安备 44130202000953号
粤公网安备 44130202000953号