(本小题满分12分)如下图所示,某海轮以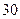 海里/小时的速度航行,在
海里/小时的速度航行,在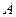 点测得海面上油井
点测得海面上油井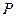 在南偏东
在南偏东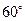 ,向北航行
,向北航行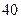
 分钟后到达
分钟后到达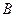 点,测得油井
点,测得油井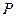 在南偏东
在南偏东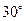 ,海轮改为北偏东
,海轮改为北偏东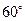 的航向再行驶
的航向再行驶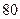 分钟到达
分钟到达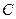 点,求
点,求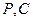 间的距离.
间的距离.
相关知识点
推荐套卷
(本小题满分12分)如下图所示,某海轮以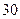 海里/小时的速度航行,在
海里/小时的速度航行,在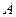 点测得海面上油井
点测得海面上油井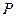 在南偏东
在南偏东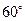 ,向北航行
,向北航行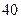
 分钟后到达
分钟后到达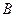 点,测得油井
点,测得油井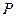 在南偏东
在南偏东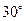 ,海轮改为北偏东
,海轮改为北偏东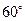 的航向再行驶
的航向再行驶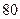 分钟到达
分钟到达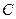 点,求
点,求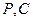 间的距离.
间的距离.