高中数学几何不等式填空题

设f(x)是定义在R上的奇函数，且f(－1)＝0，当x＞0时，(x²＋1)f′(x)－2xf(x)＜0，则不等式f(x)＞0的解集为________．

己知，若恒成立，利用柯西不等式可求得实数的取值范围是         .

已知函数f(x)= 则满足不等式f(1-x²)>f(2x)的x的取值范围是　　　　.

不等式的解集为或，则实数的取值范围      ．

设，则的最小值是          

设，则的最小值为_________．

若不等式的解集为，则实数的值为          .

设x,y为实数,满足3≤xy²≤8,4≤≤9,则的最大值是　　　　　　.

设均为正实数，且，则的最小值为      ．

关于x的不等式x²－ax＋2a＜0的解集为A，若集合A中恰有两个整数，则实数a的取值范围是________．

若不等式(mx－1)［3m ²－( x + 1)m－1］≥0对任意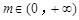恒成立，则实数x的值为    ．

某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月份至十月份销售总额至少达7000万元,则x的最小值是　　　.

不等式的解集为              

已知集合，B={x/ax²+bx+c0},若则的最小值_______.

设关于x的不等式mx²－2x－m＋1＜0对于满足|m|≤2的一切m都成立，则x的取值范围是________．