函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围;
(2)当x∈[-2,2]时,f(x)≥a恒成立,求a的取值范围.
如图,动物园要围成相同面积的长方形虎笼四间.一面可利用原有的墙,其他各面用钢筋网围成.
(1)现有可围成36m长的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
(2)若使每间虎笼的面积为24m2,则每间虎笼的长、宽各设计为多少时,可使围成的四间虎笼的钢筋网总长最小?
已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.
已知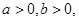 且
且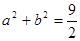 ,若
,若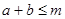 恒成立,
恒成立,
(1)求 的最小值;(2)若
的最小值;(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知f(x)=-3x2+a(6-a)x+b.
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a、b的值.
已知f(x)为二次函数,不等式f(x)+2<0的解集是 ,且对任意α、β∈R恒有f(sinα)≤0,f(2+cosβ)≥0,求函数f(x)的解析式.
,且对任意α、β∈R恒有f(sinα)≤0,f(2+cosβ)≥0,求函数f(x)的解析式.
不等式(-1)na<2+ 对任意n∈N*恒成立,求实数a的取值范围.
对任意n∈N*恒成立,求实数a的取值范围.
某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司要生产A类产品至少50件,B类产品至少140件,所需租赁费最多不超过2500元,写出满足上述所有不等关系的不等式.
(本小题满分13分)
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径成为M到N的一条“L路径”。如图所示的路径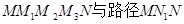 都是M到N的“L路径”。某地有三个新建的居民区,分别位于平面xOy内三点
都是M到N的“L路径”。某地有三个新建的居民区,分别位于平面xOy内三点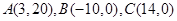 处。现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心。
处。现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心。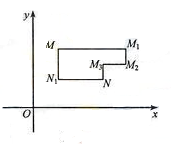
(I)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明);
(II)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度值和最小。