(本小题满分12分)如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为60°,再由点C沿东偏北75°方向走20米到达位置D,测得∠BDC=30°。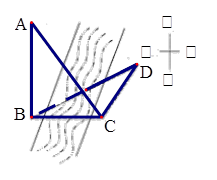
(Ⅰ)求sⅠn∠BCD的值;
(Ⅱ)求此建筑物的高度.
已知函数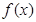 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当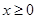 时有
时有 .
.
(1)判断函数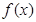 的单调性,并求使不等式
的单调性,并求使不等式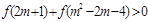 成立的实数
成立的实数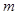 的取值范围.
的取值范围.
(2)若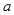 、
、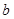 、
、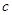 分别是
分别是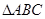 的三个内角
的三个内角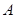 、
、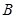 、
、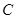 所对的边,
所对的边,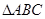 面积
面积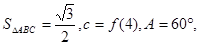 求
求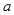 、
、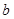 的值;
的值;
(本小题满分12分)如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20 m,求山高CD.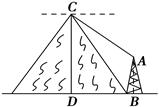
设函数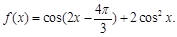
(1)求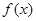 的最大值,并写出使
的最大值,并写出使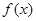 取最大值时x的集合;
取最大值时x的集合;
(2)已知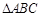 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若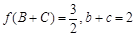 ,求a的最小值.
,求a的最小值.
如图,甲船以每小时 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?(结论保留根号形式)
海里,问乙船每小时航行多少海里?(结论保留根号形式)