高中数学西姆松定理试题

在△ABC中，角A、B、C的对边分别为、、．已知向量，，且．
（1）求的值；
（2）若，求△ABC的面积S．

（本小题满分12分） 在中，角所对的边分别为．，．
（1）求角的大小；
（2）若最大边的边长为，求最小边的边长及的面积．

在中，，，cm，则     cm.  

在△ABC中，a、b、c分别是角A、B、C的对边，向量，，且
（1）求角B的大小；
（2）设 （），且f（x）的最小正周期为π，求f（x）的单调区间．

（本小题满分12分）已知向量，，函数．
（1）求函数的对称中心；
（2）在中，分别是角的对边，且，，，且，求的值．

在中，内角所对的边长分别是。若，则的形状为（    ）

A．等腰三角形	B．直角三角形
C．等腰直角三角形	D．等腰或直角三角形

（本小题满分12分）在中，角A、B、C所对的边分别为，且
（1）求角C的大小；
（2）若的面积，求的值.

已知向量，，函数．
（1）求函数的最小正周期与值域；
（2）已知，，分别为内角， ，的对边，其中为锐角，，，且，求，和的面积．

以下四个命题：
①在中,内角A,B,C的对边分别为,且，则；
②设是两个非零向量且，则存在实数λ，使得；
③方程在实数范围内的解有且仅有一个；
④且，则；  
其中正确的命题序号为               。

.给出下列结论：
①函数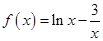在区间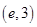上有且只有一个零点；
②已知l是直线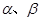，是两个不同的平面.若；
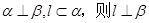③已知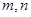表示两条不同直线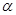，表示平面.若；
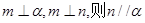④在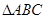中，已知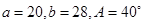，在求边c的长时有两解.
其中所有正确结论的序号是：            .

已知函数．
（1）求函数的单调递增区间；
（2）在中，内角所对边的长分别是，若，求的面积的值．

已知的重心为G，角A，B，C所对的边分别为，若，则

A．1：1:1

B．

C．

D．

（本小题满分12分）已知分别为三个内角的对边，.
（1）求的大小；
（2）若= 7，求的周长的取值范围．

已知的内角的对边分别为，．
（1）若，，求的值；
（2）若，求的值．

（本小题满分12分）在中，角所对的边为，且满足
（1）求角的值；
（2）若且，求的取值范围．