如果函数 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;
(2)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 在
在 上有最大值;
上有最大值;
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若 与
与 交点个数为2013,求
交点个数为2013,求 的值.
的值.
已知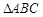 的三内角分别为
的三内角分别为 ,向量
,向量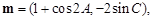
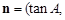
 ,记函数
,记函数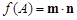 .
.
(1)若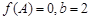 ,求
,求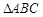 的面积;
的面积;
(2)若关于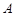 的方程
的方程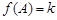 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
定义:对于函数 ,若存在非零常数
,若存在非零常数 ,使函数
,使函数 对于定义域内的任意实数
对于定义域内的任意实数 ,都有
,都有 ,则称函数
,则称函数 是广义周期函数,其中称
是广义周期函数,其中称 为函数
为函数 的广义周期,
的广义周期, 称为周距.
称为周距.
(1)证明函数 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距 的值;
的值;
(2)试求一个函数 ,使
,使 (
( 为常数,
为常数, )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期 和周距
和周距 ;
;
(3)设函数 是周期
是周期 的周期函数,当函数
的周期函数,当函数 在
在 上的值域为
上的值域为 时,求
时,求 在
在 上的最大值和最小值.
上的最大值和最小值.
已知函数 ,满足
,满足 .
.
(1)求常数c的值;
(2)解关于 的不等式
的不等式 .
.
已知函数 (
( ).
).
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)若 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若 ,求函数
,求函数 的值域.
的值域.
已知函数 .
.
(1)解关于 的不等式
的不等式 ;
;
(2)若 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
已知函数 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1.
(1)求实数a的值,并求函数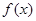 的单调区间,
的单调区间,
(2)若不等式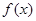 ≥k在区间
≥k在区间 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围.
设函数
(I)求函数 的单调区间;
的单调区间;
(II)若不等式 (
( )在
)在 上恒成立,求
上恒成立,求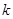 的最大值.
的最大值.
已知函数 (
( ).
).
(1)证明:当 时,
时, 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时 的单调区间;
的单调区间;
(2)已知函数 ,函数
,函数 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录.为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足 (其中
(其中 ,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为
,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为 元/件.
元/件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
(小题满分14分)已知定义域为R的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知函数 .
.
(1) 试说明函数 的图像是由函数
的图像是由函数 的图像经过怎样的变换得到的;
的图像经过怎样的变换得到的;
(2) (理科)若函数 ,试判断函数
,试判断函数 的奇偶性,并用反证法证明函数
的奇偶性,并用反证法证明函数 的最小正周期是
的最小正周期是 ;
;
(3) 求函数 的单调区间和值域.
的单调区间和值域.