德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则关于函数
为有理数集,则关于函数 有如下四个结论:
有如下四个结论:
① ;
;
②函数 是偶函数;
是偶函数;
③任取一个不为零的有理数 ,
, 对任意的
对任意的 恒成立;
恒成立;
④存在三个点 ,
, ,
, ,使得
,使得 为等边三角形.
为等边三角形.
其中正确结论的个数是()
A. |
B. |
C. |
D. |
设 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若函数
上的两个函数,若函数 上有两个不同的零点,则称
上有两个不同的零点,则称 和
和 在
在 上是“关联函数”,区间
上是“关联函数”,区间 称为“关联区间”。若
称为“关联区间”。若 上是“关联函数”,则m的取值范围为()
上是“关联函数”,则m的取值范围为()
A. |
B. |
C. |
D. |
能够把椭圆 :
: 的周长和面积同时分为相等的两部分的函数
的周长和面积同时分为相等的两部分的函数 称为椭圆
称为椭圆 的“亲和函数”,下列函数是椭圆
的“亲和函数”,下列函数是椭圆 的“亲和函数”的是()
的“亲和函数”的是()
A. |
B. |
C. |
D. |
若存在实常数 和
和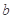 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数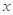 都满足:
都满足: 和
和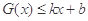 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”,已知函数
的“隔离直线”,已知函数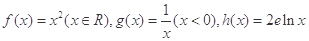 ,有下列命题:
,有下列命题:
①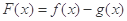 在
在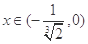 内单调递增;
内单调递增;
②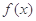 和
和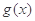 之间存在“隔离直线”,且
之间存在“隔离直线”,且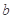 的最小值为
的最小值为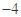 ;
;
③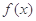 和
和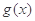 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的取值范围是
的取值范围是 ;
;
④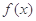 和
和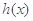 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”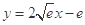 .
.
其中真命题的个数有()
A. 个 个 |
B. 个 个 |
C. 个 个 |
D.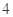 个 个 |
对于函数 和
和 ,设
,设 ,
, ,若存在
,若存在 ,使得
,使得 ,则称
,则称 与
与 互为“零点相邻函数”.若函数
互为“零点相邻函数”.若函数 与
与 互为“零点相邻函数”,则实数
互为“零点相邻函数”,则实数 的取值范围是()
的取值范围是()
A. |
B. |
C. |
D. |
如果对定义在R上的函数 ,对任意
,对任意 ,都有
,都有 则称函数
则称函数 为“H函数”.给出下列函数:
为“H函数”.给出下列函数:
① ;
;
② ;
;
③ ;
;
④ .
.
其中函数式“H函数”的个数是()
| A.4 | B.3 | C.2 | D.1 |
定义在 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在 上的如下函数:
上的如下函数:
① ②
② ③
③ ④
④ .
.
则其中是“保等比数列函数”的 的序号为
的序号为
| A.①② | B.③④ | C.①③ | D.②④ |
对函数 ,在使
,在使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最大值叫做函数
的最大值叫做函数 的下确界.现已知定义在R上的偶函数
的下确界.现已知定义在R上的偶函数 满足
满足 ,当
,当 时,
时, ,则
,则 的下确界为 ()
的下确界为 ()
A. |
B. |
C. |
D. |
若函数 满足:在定义域D内存在实数
满足:在定义域D内存在实数 ,使得
,使得 成立,则称函数
成立,则称函数 为“1的饱和函数”.给出下列四个函数:①
为“1的饱和函数”.给出下列四个函数:① ;②
;② ;③
;③ ;④
;④ .其中是“1的饱和函数”的所有函数的序号为().
.其中是“1的饱和函数”的所有函数的序号为().
| A.①③ | B.②④ | C.①② | D.③④ |
对于定义域和值域均为[0,1]的函数f(x),定义 ,
, ,…,
,…, ,n=1,2,3,….满足
,n=1,2,3,….满足 的点x∈[0,1]称为f的
的点x∈[0,1]称为f的 阶周期点.设
阶周期点.设 则f的
则f的 阶周期点的个数是
阶周期点的个数是
| A.2n | B.2(2n-1) | C.2n | D.2n2 |