设函数 的定义域为 , 是 的极大值点, ,以下结论一定正确的是()
| A. | , | B. | 是 的极小值点 |
| C. | 是 的极小值点 | D. | 是 的极小值点 |
如图,点 从点
从点 出发,分别按逆时针方向沿周长均为
出发,分别按逆时针方向沿周长均为 的正三角形、正方形运动一周,
的正三角形、正方形运动一周, 两点连线的距离
两点连线的距离 与点
与点 走过的路程
走过的路程 的函数关系分别记为
的函数关系分别记为 ,定义函数
,定义函数 对于函数
对于函数 ,下列结论正确的个数是( )
,下列结论正确的个数是( )
① ;
;
②函数 的图像关于直线
的图像关于直线 对称;
对称;
③函数 值域为
值域为 ;
;
④函数 在区间
在区间 上单调递增.
上单调递增.
| A.1 | B.2 | C.3 | D.4 |
已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若函数 的最小值为
的最小值为 ,求
,求 的最大值;
的最大值;
(3)若函数 的最小值为
的最小值为 ,
, 为
为 定义域
定义域 内的任意两个值,试比较
内的任意两个值,试比较  与
与 的大小.
的大小.
对于函数 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(Ⅰ)已知二次函数 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(Ⅱ)若 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;
(Ⅲ)若 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
设 ,函数
,函数 在
在 单调递减,则
单调递减,则 ( )
( )
A.在 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
B.在 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C.在 上单调递增,在 上单调递增,在 上单调递增 上单调递增 |
D.在 上单调递减,在 上单调递减,在 上单调递减 上单调递减 |
已知函数
(1)当 时,求
时,求 在
在 上的最小值;
上的最小值;
(2)若函数 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(3)若关于 的方程
的方程 在区间
在区间 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数 的取值范围.
的取值范围.
函数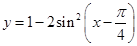 是( )
是( )
A.最小正周期为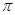 的偶函数 的偶函数 |
B.最小正周期为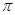 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的奇函数 的奇函数 |
已知函数 的两个极值点分别为
的两个极值点分别为 ,且
,且 ,
, ,点
,点 表示的平面区域为
表示的平面区域为 ,若函数
,若函数 的图像上存在区域
的图像上存在区域 内的点,则实数
内的点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
对于函数 ,如果存在区间
,如果存在区间 ,同时满足下列条件:①
,同时满足下列条件:① 在
在 内是单调的;②当定义域是
内是单调的;②当定义域是 时,
时, 的值域也是
的值域也是 ,则称
,则称 是该函数的“和谐区间”.若函数
是该函数的“和谐区间”.若函数 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |