已知函数
 ,给出下列命题:
,给出下列命题:
(1) 必是偶函数;
必是偶函数;
(2)当 时,
时, 的图象关于直线
的图象关于直线 对称;
对称;
(3)若 ,则
,则 在区间
在区间 上是增函数;
上是增函数;
(4) 有最大值
有最大值 .
.
其中正确的命题序号是( )
| A.(3) | B.(2)(3) | C.(3)(4) | D.(1)(2)(3) |
已知函数f(x)="a" sinx-bcosx (a、b为常数,a≠0,x∈R)在x= 处取得最小值,则函数y=f(
处取得最小值,则函数y=f( -x)是( )
-x)是( )
| A.偶函数且它的图象关于点(π,0)对称 |
B.偶函数且它的图象关于点( ,0)对称 ,0)对称 |
C.奇函数且它的图象关于点( ,0)对称 ,0)对称 |
| D.奇函数且它的图象关于点(π,0)对称 |
已知函数 在
在 处取得极值,且
处取得极值,且 恰好是
恰好是 的一个零点.
的一个零点.
(Ⅰ)求实数 的值,并写出函数
的值,并写出函数 的单调区间;
的单调区间;
(Ⅱ)设 、
、 分别是曲线
分别是曲线 在点
在点 和
和 (其中
(其中 )处的切线,且
)处的切线,且 .
.
①若 与
与 的倾斜角互补,求
的倾斜角互补,求 与
与 的值;
的值;
②若 (其中
(其中 是自然对数的底数),求
是自然对数的底数),求 的取值范围.
的取值范围.
已知函数 若直线
若直线 与函数
与函数 的图象有两个不同的交点,则实数
的图象有两个不同的交点,则实数 的取值范围是 .
的取值范围是 .
已知函 数 .
.
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数 的单调区间;
的单调区间;
(2)若对于 都有
都有 成立,试求
成立,试求 的取值范围;
的取值范围;
(3)记 .当
.当 时,函数
时,函数 在区间
在区间 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围.
函数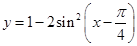 是( )
是( )
A.最小正周期为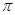 的偶函数 的偶函数 |
B.最小正周期为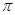 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的奇函数 的奇函数 |
已知函数 的两个极值点分别为
的两个极值点分别为 ,且
,且 ,
, ,点
,点 表示的平面区域为
表示的平面区域为 ,若函数
,若函数 的图像上存在区域
的图像上存在区域 内的点,则实数
内的点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
对于函数 ,如果存在区间
,如果存在区间 ,同时满足下列条件:①
,同时满足下列条件:① 在
在 内是单调的;②当定义域是
内是单调的;②当定义域是 时,
时, 的值域也是
的值域也是 ,则称
,则称 是该函数的“和谐区间”.若函数
是该函数的“和谐区间”.若函数 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |