高中数学不定方程和方程组填空题

给出下列结论：
①函数在区间上有且只有一个零点；
②已知l是直线，是两个不同的平面．若；
③已知表示两条不同直线，表示平面．若；
④在中，已知，在求边c的长时有两解．
其中所有正确结论的序号是：           .

已知函数对任意的满足，且当时，．若有4个零点，则实数的取值范围是            ．

．下列说法：
①函数的零点只有1个且属于区间；
②若关于的不等式恒成立，则；
③函数的图像与函数的图像有3个不同的交点；
④函数的最小值是1．
正确的有          ．（请将你认为正确说法的序号都写上）

定义函数，则函数在区间内的所有零点的和为       .

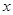若关于的方程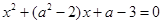的一根比2小且另一根比2大，则的取值范围是____________．

设常数使方程 在闭区间上恰有三个解，则     ．

设函数的根都在区间[-2，2]内，且函数在区间（0，1）上单调递增，则b的取值范围是            。

函数f（x）＝2^x－5的零点所在区间为[m，m＋1]（m∈N），则m＝         ．

已知函数的一个零点比大，一个零点比小，则实数的取值范围           ．

己知函数f（x）=|lnx|，，则方程|f（x）+g（x）| =1实根的个数为      个．

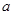若函数不存在零点，则实数的取值范围是    ．

定义在上的函数满足：①当时，；②．设关于的函数的零点从小到大依次为．若，则   ________ ；若，则________________．

若函数有两个零点，则应满足的充要条件是         .

设是函数的零点，且，，则k=           ．

已知直线与曲线恰有四个不同的交点，则实数k的取值范围为     ．