高中数学不定方程和方程组填空题

已知f(x)=ax²+bx+c(a≠0)，g(x)=f[f(x)]，其中真命题的个数是_________个。 
①若f(x)无零点，则g(x)>0对x∈R成立；
②若f(x)有且只有一个零点，则g(x)必有两个零点；
③若方程f(x)=0有两个不等实根，则方程g(x)=0不可能无解。

若函数在实数集上的图象是连续不断的，且对任意实数存在常数使得恒成立，则称是一个“关于函数”．现有下列“关于函数”的结论：
①常数函数是“关于函数”；
②“关于2函数”至少有一个零点；
③是一个“关于函数”．
其中正确结论的序号是               ．

已知是满足条件的五个不同的整数，若是关于x的方程的整数根，则的值为

函数 的图象和函数的图象的交点个数是     。 

若一元二次方程解为,则分解因式    

若函数的零点个数为，则              ．

若函数f（x）＝3|cosx|－cosx＋m, x∈（0, 2π），有两个互异零点，则实数m的取值范围是_________．

已知，则        ．

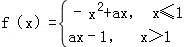若∃x₁，x₂∈R，x₁≠x₂，使得f（x₁）=f（x₂）成立，则实数a的取值范围是      ．

已知函数，，则函数的零点个数为             ．

函数f（x）=ax³﹣3x²+1，若f（x）=0存在唯一正实数根x₀，则a取值范围是       ．

己知函数f（x）=|lnx|，，则方程|f（x）+g（x）| =1实根的个数为      个．

某同学在借助计算器求“方程的近似解（精确到0．1）”时，设，算得；在以下过程中，他用“二分法”又取了4个的值，计算了其函数值的正负，并得出判断：方程的近似解是．
那么他又取的的4个值分别依次是                                     ．

若实数满足，则的取值范围是____________________.

已知方程的解所在区间为，则=      ．