已知f(x)=ax2+bx+c(a≠0)，g(x)=f[f(x)]，其中真命题的个数是_________个。
①若f(x)无零点，则g(x)>0对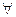
x∈R成立；
②若f(x)有且只有一个零点，则g(x)必有两个零点；
③若方程f(x)=0有两个不等实根，则方程g(x)=0不可能无解。
，
，则
_______________________.
中,
分别为角
所对的边，若
，则
.
时，不等式
恒成立，则m的取值范围是____.
，
，
．则下列不等式：①
； ②
； ③
；④
.其中成立的是．(写出所有正确命题的序号)
中，已知
，
，则该数列的前15项的和
____.相关知识点
推荐套卷
已知f(x)=ax2+bx+c(a≠0)，g(x)=f[f(x)]，其中真命题的个数是_________个。
①若f(x)无零点，则g(x)>0对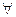x∈R成立；
②若f(x)有且只有一个零点，则g(x)必有两个零点；
③若方程f(x)=0有两个不等实根，则方程g(x)=0不可能无解。
粤公网安备 44130202000953号