对于任意的两个实数对 (a,b) 和 (c,d),规定:(a,b) = (c,d)当且仅当a = c,b = d;运算“Ä”为:(a,b) Ä (c,d) = (ac+bd,bc-ad);运算“Å”为:(a,b) Å (c,d) = (a + c,b + d),设x ,yÎ R,若(3,4) Ä (x ,y) = (11,-2),则(3,4) Å (x ,y) =( )
| A.(4,6) | B.(4,6) | C.(2,2) | D.(5,5) |
已知函数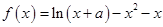 在
在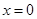 处取得极值
处取得极值
(1)求实数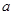 的值;
的值;
(2)若关于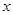 的方程
的方程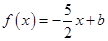 在区间
在区间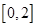 上有两个不同的实根,求实数
上有两个不同的实根,求实数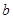 的取值范围.
的取值范围.
已知 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, .
.
(1)求 ,
, 的值;
的值;
(2)求 的解析式;并画出简图;
的解析式;并画出简图;
(3)利用图象讨论方程 的根的情况(只需写出结果,不要解答过程).
的根的情况(只需写出结果,不要解答过程).
已知函数 (
( 为自然对数的底数,
为自然对数的底数, ).
).
(1)判断曲线 在点
在点 处的切线与曲线
处的切线与曲线 的公共点个数;
的公共点个数;
(2)当 时,若函数
时,若函数 有两个零点,求a的取值范围.
有两个零点,求a的取值范围.
(本小题满分12分)设关于 的方程
的方程 ,
,
(1)若方程有实数解,求实数 的取值范围;
的取值范围;
(2)当方程有实数解时,讨论方程实根的个数,并求出方程的解。