设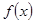 是定义在区间
是定义在区间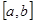 上的函数,且
上的函数,且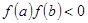 ,则方程
,则方程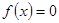 在区间
在区间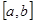 上( )
上( )
| A.至少有一实根 | B.至多有一实根 |
| C.没有实根 | D.必有唯一实根 |
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f″(x)是函数y=f(x)的导数y=f ′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.如“函数f(x)=x3-3x2+3x对称中心为点 (1,1)”请你将这一发现
′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.如“函数f(x)=x3-3x2+3x对称中心为点 (1,1)”请你将这一发现
已知f(x)=ax2+bx+c(a≠0),g(x)=f[f(x)],其中真命题的个数是_________个。
①若f(x)无零点,则g(x)>0对 x∈R成立;
x∈R成立;
②若f(x)有且只有一个零点,则g(x)必有两个零点;
③若方程f(x)=0有两个不等实根,则方程g(x)=0不可能无解。
已知函数 满足
满足 ,且
,且 有唯
有唯
一实数解。
(1)求 的表达式 ;
的表达式 ;
(2)记 ,且
,且 =
= ,求数列
,求数列 的通项公式。
的通项公式。
(3)记  ,数列{
,数列{ }的前
}的前  项和为
项和为  ,是否存在k∈N*,使得
,是否存在k∈N*,使得
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
小明用下面的方法求出方程 的解,请你仿照他的方法求出下面方程
的解,请你仿照他的方法求出下面方程 的解为 ;
的解为 ;
| 方程 |
换元法得新方程 |
解新方程 |
检验 |
求原方程的解 |
 |
令 则  |
t=2 |
t ="2" > 0 |
 所以x=4 |
若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为( )
| A.1.2 | B.1.3 | C.1.4 | D.1.5 |