设命题p:函数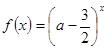 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在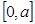 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求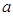 的取值范围.
的取值范围.
设命题p:函数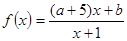 在(0,+
在(0,+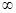 )上是增函数;命题q:方程
)上是增函数;命题q:方程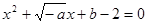 有两个不相等的负实数根,若p
有两个不相等的负实数根,若p q是真命题。
q是真命题。
(1)求点P(a,b)的轨迹图形的面积;
(2)求a+5b的取值范围。
已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈[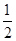 ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+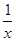 >
>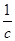 恒成立.如果p或q为真命题,p且q为假命题.求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题.求c的取值范围.
(本小题满分10分)
命题p:对任意实数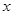 都有
都有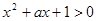 恒成立;命题q :关于
恒成立;命题q :关于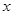 的方程
的方程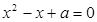 有实数根.若“p或q”为真命题,“p且q”为假命题,求实数
有实数根.若“p或q”为真命题,“p且q”为假命题,求实数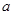 的取值范围。
的取值范围。
本小题12分)命题p: 函数y=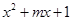 在(-1, +
在(-1, + )上单调递增, 命题
)上单调递增, 命题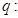 函数y=lg[
函数y=lg[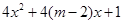 ]的定义域为R
]的定义域为R
(1) 若“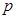 或
或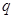 ”为真命题,求
”为真命题,求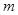 的取值范围;
的取值范围;
(2) 若“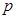 或
或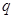 ”为真命题,“
”为真命题,“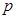 且
且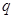 ”为假命题,求
”为假命题,求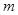 的取值范围
的取值范围
(本小题满分12分)设 是实数,对函数
是实数,对函数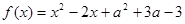 和抛物线
和抛物线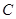 :
: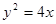 ,有如下两个命题:
,有如下两个命题: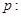 函数
函数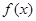 的最小值小于0;
的最小值小于0;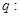 抛物线
抛物线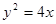 上的点
上的点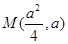 到其准线的距离
到其准线的距离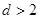 .
.
已知“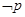 ”和“
”和“
 ”都为假命题,求
”都为假命题,求 的取值范围.
的取值范围.
已知a>0且a≠1,设命题p:函数y=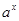 +1在R上单调递减,命题q:曲线y=
+1在R上单调递减,命题q:曲线y=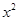 +(2a-3)x+1与x轴交于不同的两点,如果“p∨q”为真,且“p∧q”为假,求a的取值范围.
+(2a-3)x+1与x轴交于不同的两点,如果“p∨q”为真,且“p∧q”为假,求a的取值范围.