高中数学随机思想的发展解答题

本小题满分12分）(注意:在试题卷上作答无效)

在进行一项掷骰子放球的游戏中规定：若掷出1点或2点，则在甲盒中放一球；否则，在乙盒中放一球。现在前后一共掷了4次骰子，设、分别表示甲、乙盒子中球的个数。
（Ⅰ）求的概率；
（Ⅱ）若求随机变量的分布列和数学期望。

济南市开展支教活动，有五名教师被随机的分到A、B、C三个不同的乡镇中学，且每个乡镇中学至少一名教师，
（1）求甲乙两名教师同时分到一个中学的概率；
（2）求A中学分到两名教师的概率；
（3）设随机变量X为这五名教师分到A中学的人数，求X的分布列和期望．

某次月考数学第Ⅰ卷共有8道选择题，每道选择题有4个选项，其中只有一个是正
确的；评分标准为：“每题只有一个选项是正确的，选对得5分，不选或选错得0分．”某考生每道题都给出一个答案，已确定有5道题的答案是正确的，而其余3道题中，有一道题可判断出两个选项是错误的，有一道题可以判断出一个选项是错误的，还有一道题因不了解题意而乱猜，试求该考生：
（Ⅰ）得40分的概率；
（Ⅱ）得多少分的可能性最大？
（Ⅲ）所得分数的数学期望．

（本小题满分12分）
在甲、乙等7个选手参加的一次演讲比赛中，采用抽签的方式随机确定每个选手的演出顺序（序号为1,2,……7），求：
（1）甲、乙两个选手的演出序号至少有一个为奇数的概率；
（2）甲、乙两选手之间的演讲选手个数的分布列与期望.

第十一届西博会于2010年10月22日至26日在蓉举行，本届西博会以“绿色改变生活，技术引领发展”为主题。如此重要的国际盛会，自然少不了志愿者这支重要力量，“志愿者，西博会最亮丽的风景线”，通过他们的努力和付出，已把志愿者服务精神的种子播撒到人们心中。某大学对参加了本次西博会的该校志愿者实施“社会教育实践”学分考核，因该批志愿者表现良好，该大学决定考核只有合格和优秀两个等次，若某志愿者考核为合格，授予0.5个学分；考核为优秀，授予1个学分。假设该校志愿者甲、乙、丙考核为优秀的概率分别为、、，他们考核所得的等次相互独立。
（I）求在这次考核中，志愿者甲、乙、两三人中至少有一名考核为优秀的概率；
（II）求在这次考核中甲、乙、丙三名志愿者所得学分之和为整数的概率。

（本小题满分12分）
某辆载有4位乘客的公共汽车在到达终点前还有3个停靠点（包括终点站），若车上每位乘客在所剩的每一个停靠点下车的概率均为，用表示这4位乘客在终点站下车的人数，求：
(1)随机变量的分布列；
(2)随机变量的数学期望.

：某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为，只选修甲和乙的概率是，至少选修一门的概率是，用表示小张选修的课程门数和没有选修的课程门数的乘积.
（Ⅰ）求学生小张选修甲的概率；
（Ⅱ）记“函数 为上的偶函数”为事件，求事件的概率；
（Ⅲ）求的分布列和数学期望。           

(（本小题满分12分） 某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上的40件产品作为样本称出它们的重量（单位：克），重量的分组区间为（490,495]，（495,500]，……，（510,515]，由此得到样本的频率分布直方图，如图4所示.
（Ⅰ）根据频率分布直方图，求重量超过500 克的产品数量;
（Ⅱ）在上述抽取的40件产品中任取2件，设Y为重量超过505克的产品数量， 求Y的分布列及数学期望.

．（本小题12 分）
有一个箱子内放有3个红球、1个白球、1个黄球，现从箱子里任意取球，每次只取一个，取后不放回.
①求前两次先后取到一个红球和一个白球的概率；
②若取得红球则停止取球，求取球次数的分布列及期望.

（本小题满分14分）
桌面上有三颗均匀的骰子（6个面上分别标有数字1，2，3，4，5，6）。重复下面的操作，直到桌面上没有骰子：将骰子全部抛掷，然后去掉那些朝上点数为奇数的骰子。记操作三次之内（含三次）去掉的骰子的颗数为X.
（1）求；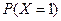
（2）求X的分布列及期望.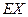

（本小题满分12分）
某市有A、B两所示范高中响应政府号召，对该市甲、乙两个教育落后地区开展支教活动．经上级研究决定：向甲地派出3名A校教师和2名B校教师，向乙地派出3名A校教师和3名B校教师．由于客观原因，需从拟派往甲、乙两地的教师中各自任选一名互换支教地区．
（Ⅰ）求互换后两校派往两地区教师人数不变的概率；
（Ⅱ）求互换后A校教师派往甲地人数的分布列和数学期望．

（本小题满分13分）
一个袋中装有个形状大小完全相同的小球，球的编号分别为.
（Ⅰ）若从袋中每次随机抽取1个球，有放回的抽取2次，求取出的两个球编号之和为6的概率；
（Ⅱ）若从袋中每次随机抽取个球，有放回的抽取3次，求恰有次抽到号球的概率；
（Ⅲ）若一次从袋中随机抽取个球，记球的最大编号为，求随机变量的分布列.

在一个盒子中有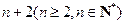个球，其中2个球的标号是不同的偶数，其余n个球的标号是不同的奇数。甲乙两人同时从盒子中各取出2个球，若这4个球的标号之和为奇数，则甲胜；若这4个球的标号之和为偶数，则乙胜。规定：胜者得2分，负者得0分。
（I）当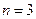时，求甲的得分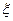的分布列和期望；
（II）当乙胜概率为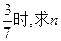的值

(本小题满分12分)
四个大小相同的小球分别标有数字1、1、2、2，把它们放在一个盒子里，从中任意摸出两个小球，它们所标有的数字分别为、，记；
(Ⅰ)求随机变量的分布列和数学期望；
(Ⅱ)设“函数在区间上有且只有一个零点”为事件，求事件发生的概率．

（本小题满分12分）一射击测试每人射击三次，每击中目标一次记10分。没有击中记0分，某人每次击中目标的概率为
（I）求此人得20分的概率；（II）求此人得分的数学期望与方差。