(本小题满分12分)袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为 ,求E
,求E .
.
(本大题9分)袋中有2个红球,n个白球,各球除颜色外均相同.已知从袋中摸出2个球均为白球的概率为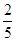 ,(Ⅰ)求n;(Ⅱ)从袋中不放回的依次摸出三个球,记ξ为相邻两次摸出的球不同色的次数(例如:若取出的球依次为红球、白球、白球,则ξ=1),求随机变量ξ的分布列及其数学期望Eξ.
,(Ⅰ)求n;(Ⅱ)从袋中不放回的依次摸出三个球,记ξ为相邻两次摸出的球不同色的次数(例如:若取出的球依次为红球、白球、白球,则ξ=1),求随机变量ξ的分布列及其数学期望Eξ.
(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
| 射手甲 |
射手乙 |
||||||
| 环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
| 概率 |
 |
 |
 |
概率 |
 |
 |
 |
(Ⅰ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅱ)若两个射手各射击1次,记所得的环数之和为 ,求
,求 的分布列和期望.
的分布列和期望.
为抗击金融风暴,某系统决定对所属企业给予低息贷款的扶持,该系统制定了评分标准,并根据标准对企业进行评估,然后依据评估得分将这些企业分别定为优秀、良好、合格、不合格四个等级,并根据等级分配相应的低息贷款数额,为了更好地掌握贷款总额,该系统随机抽查了所属的部分企业.一下图表给出了有关数据(将频率看做概率)
(1)任抽一家所属企业,求抽到的企业等级是优秀或良好的概率;
(2)对照标准,企业进行了整改.整改后,如果优秀企业数量不变,不合格企业、合格企业、良好企业的数量成等差数列.要使所属企业获得贷款的平均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数百分比的最大值是多少?

第26届世界大学生夏季运动会将于2011年8月12日至23日在深圳举行,为了搞好接待工作,组委会在某学院招募了 名男志愿者和
名男志愿者和 名女志愿者,调查发现,这
名女志愿者,调查发现,这 名志愿者的身高如下:(单位:cm )
名志愿者的身高如下:(单位:cm )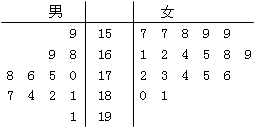
若身高在 cm以上(包括
cm以上(包括 cm)定义为“高个子”,身高在
cm)定义为“高个子”,身高在 cm以下定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
cm以下定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取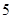 人,再从这
人,再从这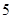 人中选
人中选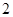 人,则至少有一人是“高个子”的概率是多少?
人,则至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选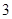 名志愿者,用
名志愿者,用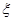 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出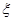 的分布列,并求
的分布列,并求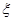 的数学期望.
的数学期望.
在一个盒子中,放有标号分别为 ,
, ,
, 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为 、
、 ,记
,记 .
.
(Ⅰ)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量 的分布列和数学期望.
的分布列和数学期望.
(12分)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;
(2)求在2次游戏中获奖次数X的分布列及数学期望E(X).
在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛.
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为 (
( 所有取值为0,1,2,3...,10)的概率分别为
所有取值为0,1,2,3...,10)的概率分别为 、
、 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
 |
0 |
0 |
0 |
0 |
0.06 |
0.04 |
0.06 |
0.3 |
0.2 |
0.3 |
0.04 |
 |
0 |
0 |
0 |
0 |
0.04 |
0.05 |
0.05 |
0.2 |
0.32 |
0.32 |
0.02 |
①1,2号运动员各射箭一次,求两人中至少有一人命中9环的概率;
②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
某商场准备在伦敦奥运会期间举行促销活动.根据市场行情,该商场决定从3种品牌的服装类商品、2种品牌的家电类商品、4种品牌的日用类商品中,任选出3种商品进行促销活动.
(Ⅰ)求选出的3种商品中至少有一种是日用类商品的概率;
(Ⅱ)商场对选出的家电类商品采用的促销方案是有奖销售,即在该类商品成本价的基础上每件提高180元作为售价销售给顾客,同时给该顾客3次抽奖的机会,若中奖一次,就可以获得一次奖金.假设该顾客每次抽奖时获奖的概率都是 ,每次中奖与否互不影响,且每次获奖时的奖金数额都为
,每次中奖与否互不影响,且每次获奖时的奖金数额都为 元,求顾客购买一件此类商品时中奖奖金总额
元,求顾客购买一件此类商品时中奖奖金总额 的分布列和数学期望
的分布列和数学期望 ,并以此测算
,并以此测算 至多为多少时,此促销方案使商场不会亏本?
至多为多少时,此促销方案使商场不会亏本?
.(本小题10分)
在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:(1)该顾客中奖的概率;(2)该顾客获得的奖品总价值 (元)的概率分布列和期望
(元)的概率分布列和期望 .
.
(本小题满分12分)某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
(1)从 三个社区中各选一人,求恰好有2人是低碳族的概率;
三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列和期望EX.
3个同学分别从a,b,c,d四门校本课程中任选其中一门,每个同学选哪一门互不影响;(I)求3个同学选择3门不同课程的概率;(II)求恰有2门课程没有被选择的概率;(Ⅲ)求选择课程a的同学个数的分布列及数学期望.
从甲地到乙地一天共有A、B 两班车,由于雨雪天气的影响,一段时间内A 班车正点到达乙地的概率为0.7,B 班车正点到达乙地的概率为0.75。
(1)有三位游客分别乘坐三天的A 班车,从甲地到乙地,求其中恰有两名游客正点到达的概率(答案用小数表示)。
(2)有两位游客分别乘坐A、B 班车,从甲地到乙地,求其中至少有1 人正点到达的概率(答案用小数表示)。
甲箱中放有 个红球与
个红球与 个白球(
个白球( ,且
,且 ),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
(Ⅰ)记取出的3个球颜色全不相同的概率为 ,求当
,求当 取得最大值时的
取得最大值时的 ,
, 的值;
的值;
(Ⅱ)当 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数 的期望
的期望 。
。