[山东]2013届山东省兖州市高三9月入学诊断理科数学试卷
设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A B,则集合
B,则集合 中的元素共有( )
中的元素共有( )
| A. 3个 | B. 4个 | C. 5个 | D. 6个 |
对于函数 ,
,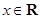 ,“
,“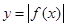 的图象关于
的图象关于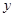 轴对称”是“
轴对称”是“ 是奇函数”的( )
是奇函数”的( )
| A.充分不必要条件 | B.充要条件 |
| C.必要不充分条件 | D.即不充分也不必要条件 |
如图,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的 任意一点,若P为半径OC上的动点, 则 的最小值是( )
的最小值是( )
A.  B.
B.  C.
C.  D.
D. 
从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有 ( )
| A.280种 | B.240种 | C.180种 | D.96种 |
若函数 的图象在点
的图象在点 处的切线
处的切线 与圆
与圆 相交,则点
相交,则点 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.圆内 | B.圆内或圆外 | C.圆上 | D.圆外 |
.函数 (
( )的图象如右图所示,为了得到
)的图象如右图所示,为了得到 的图象,可以将
的图象,可以将 的图象( )
的图象( )
A.向右平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
已知函数
(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的内角 的对边分别为a,b,c且
的对边分别为a,b,c且 =
= ,
, ,若向量
,若向量 共线,求
共线,求 的值.
的值.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(1)求证:BD⊥平面AED;
(2)求二面角F-BD-C的余弦值.
(12分)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;
(2)求在2次游戏中获奖次数X的分布列及数学期望E(X).
设等比数列 的前
的前 项和为
项和为 ,已知
,已知 N
N ).
).
(1)求数列 的通项公式;
的通项公式;
(2)在 与
与 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 项和
项和 .
.
(12分)已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),且函数g(x)= +6x的图象关于y轴对称.
+6x的图象关于y轴对称.
(1)求m、n的值及函数y=f(x)的单调区间;
(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
 随时间
随时间 变化的可能图象是 ( )
变化的可能图象是 ( )
 ,
, ,则
,则 ( )
( )



 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的取值范围是( )
的取值范围是( )



 的值的一个框图,其中菱形判断框内应填入的条件是( )
的值的一个框图,其中菱形判断框内应填入的条件是( )




 和偶函数
和偶函数 满足
满足
 ,
, ,则
,则 ( )
( )



 的大致图象是( )
的大致图象是( )

 展开式中不含
展开式中不含 项的系数的和为 .
项的系数的和为 . ,
, ,
, ,则
,则 与
与 的夹角
的夹角 为
为  与直线x=a,y=0所围成封闭图形的面积为a,则a=____
与直线x=a,y=0所围成封闭图形的面积为a,则a=____ 中椭圆
中椭圆 :
:
 的左、右焦点分别为
的左、右焦点分别为 、
、 .其中
.其中 :
: 的焦点,点
的焦点,点 为
为 .
. 满足
满足 ,直线
,直线 ∥
∥ ,且与
,且与 、
、 两点,若
两点,若 ,求直线
,求直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号