某中学经市批准建设分校,工程从2010年底开工到2013年底完工,分三期完成,经过初步招标淘汰后,确定由甲、乙两建筑公司承建,且每期工程由两公司之一独立完成,必须在建完前一期工程后再建后一期工程,已知甲公司获得第一期,第二期,第三期工程承包权的概率分别是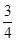 ,
,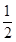 ,
,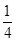 .
.
(I)求甲乙两公司均至少获得l期工程的概率;
(II)求甲公司获得的工程期数的分布列和数学期望E(X).
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:1,2,3,4,5
| 编号n |
1 |
2 |
3 |
4 |
5 |
| 成绩xn |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(注:方差s2= [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
某企业招聘工作人员,设置 、
、 、
、 三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加
三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加 组测试,丙、丁两人各自独立参加
组测试,丙、丁两人各自独立参加 组测试.已知甲、乙两人各自通过测试的概率均为
组测试.已知甲、乙两人各自通过测试的概率均为 ,丙、丁两人各自通过测试的概率均为
,丙、丁两人各自通过测试的概率均为 .戊参加
.戊参加 组测试,
组测试, 组共有6道试题,戊会其中4题.戊只能且必须选择4题作答,答对3题则竞聘成功.
组共有6道试题,戊会其中4题.戊只能且必须选择4题作答,答对3题则竞聘成功.
(Ⅰ)求戊竞聘成功的概率;
(Ⅱ)求参加 组测试通过的人数多于参加
组测试通过的人数多于参加 组测试通过的人数的概率;
组测试通过的人数的概率;
(Ⅲ)记 、
、 组测试通过的总人数为
组测试通过的总人数为 ,求
,求 的分布列和期望.
的分布列和期望.
某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名,以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”,求从这16人随机选取3人,至多有1人是“极幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
小明参加完高考后,某日路过一家电子游戏室,注意到一台电子游戏机的规则是:你可在1,2,3,4,5,6点中选一个,押上赌注a元。掷3枚骰子,如果所押的点数出现1次、2次、3次,那么原来的赌注仍还给你,并且你还分别可以收到赌注的1倍、2倍、3倍的奖励。如果所押的点数不出现,那么赌注就被庄家没收。
(1)求掷3枚骰子,至少出现1枚为1点的概率;
(2)如果小明准备尝试一次,请你计算一下他获利的期望值,并给小明一个正确的建议。
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7、8、9、10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
若将频率视为概率,回答下列问题:
(1)求表中x,y,z的值及甲运动员击中10环的概率;
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率;
(3)若甲运动员射击2次,乙运动员射击1次, 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求 的分布列及
的分布列及
节日期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段 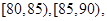

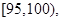
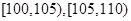 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)此调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数和中位数的估计值;
(3)若从车速在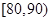 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在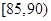 的车辆数
的车辆数 的分布列及数学期望.
的分布列及数学期望.
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层, ,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第 层第
层第 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第 层的第
层的第 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.
(Ⅰ)试求 及
及 的值,并猜想
的值,并猜想 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第 个竖直通道得到分数为
个竖直通道得到分数为 ,其中
,其中 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| |
男性 |
女性 |
合计 |
| 反感 |
10 |
|
|
| 不反感 |
|
8 |
|
| 合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是 .
.
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
| P(K2>k) |
0.05 |
0.025 |
0.010 |
0.005 |
| k |
3.841 |
5.024 |
6.635 |
7.879 |
下面的临界值表供参考:
(参考公式:K2= ,其中n="a+b+c+d)"
,其中n="a+b+c+d)"
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为
各局比赛的结果都相互独立,第 局甲当裁判.
局甲当裁判.
(I)求第 局甲当裁判的概率;
局甲当裁判的概率;
(II)求前 局中乙恰好当
局中乙恰好当 次裁判概率.
次裁判概率.
为了响应学校“学科文化节”活动,数学组举办了一场数学知识比赛,共分为甲、乙两组.其中甲组得满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生.现从得满分的学生中,每组各任选2个学生,作为数学组的活动代言人.
(1)求选出的4个学生中恰有1个女生的概率;(2)设 为选出的4个学生中女生的人数,求
为选出的4个学生中女生的人数,求 的分布列和数学期望.
的分布列和数学期望.
为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛. 该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
| 分数(分数段) |
频数(人数) |
频率 |
| [60,70) |
 |
 |
| [70,80) |
 |
 |
| [80,90) |
 |
 |
| [90,100) |
 |
 |
| 合 计 |
 |
 |
(Ⅰ)求出上表中的 的值;
的值;
(Ⅱ)按规定,预赛成绩不低于 分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一·二班在决赛中进入前三名的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
某食品加工厂甲,乙两个车间包装小食品,在自动包装传送带上每隔30分钟抽取一袋食品,称其重量并将数据记录如下:
甲:102 100 98 97 103 101 99
乙: 102 101 99 98 103 98 99
(1)食品厂采用的是什么抽样方法(不必说明理由)?
(2)根据数据估计这两个车间所包装产品每袋的平均质量;
(3)分析哪个车间的技术水平更好些?
附: