为选拔选手参加“中国汉字听写大会”,某中学举行了一次“汉字听写大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为 )进行统计.按照
)进行统计.按照 ,
, ,
, ,
, ,
, 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 ,
, 的数据).
的数据).

(1)求样本容量 和频率分布直方图中的
和频率分布直方图中的 、
、 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取3名学生参加“中国汉字听写大会”,设随机变量 表示所抽取的3名学生中得分在
表示所抽取的3名学生中得分在 内的学生人数,求随机变量
内的学生人数,求随机变量 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):规定若满意度不低于98分,测评价该教师为“优秀”.
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求 的分布列及数学期望.
的分布列及数学期望.
(本小题满分13分)某工厂生产A,B两种型号的玩具,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种玩具各100件进行检测,检测结果统计如下:
| 测试指标 |
[70,76) |
[76,82) |
[82,88) |
[88,94) |
[94,100) |
| 玩具A |
8 |
12 |
40 |
32 |
8 |
| 玩具B |
7 |
18 |
40 |
29 |
6 |
(Ⅰ)试分别估计玩具A、玩具B为正品的概率;
(Ⅱ)生产一件玩具A,若是正品可盈利40元,若是次品则亏损5元;生产一件玩具B,若是正品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件玩具A和1件玩具B所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件玩具B所获得的利润不少于140元的概率.
(本小题满分12分)根据我国发布了新修订的《环境空气质量标准》指出空气质量指数在 为优秀,人类可正常活动.某市环保局对该市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,人类可正常活动.某市环保局对该市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
, ,
,  ,
,  ,由此得到样本的空气质量指数频率分布直方图.
,由此得到样本的空气质量指数频率分布直方图.
(Ⅰ)若空气质量指数大于或等于15且小于35认为是良好的,求该市在这次监测中空气质量
为良好的天数,并根据频率分布直方图估计这一年度的空气质量指数的平均值;
(Ⅱ)如果空气质量指数不超过15,就认定空气质量为“优”,则从这一年的监测数据中随机
抽取3天的数值,其中达到“优”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题12分)据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
| 态度 调查人群 |
应该取消 |
应该保留 |
无所谓 |
| 在校学生 |
2100人 |
120人 |
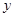 人 人 |
| 社会人士 |
600人 |
 人 人 |
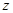 人 人 |
(1)已知在全体样本中随机抽取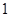 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为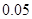 ,现用分层抽样的方法在所有参与调查的人中抽取
,现用分层抽样的方法在所有参与调查的人中抽取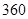 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取 人,再平均分成两组进行深入交流,求第一组中在校学生人数
人,再平均分成两组进行深入交流,求第一组中在校学生人数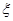 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如下图显示.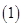 已知
已知 、
、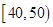 、
、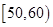 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求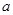 ,
,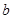 的值;
的值;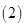 该电子商务平台将年龄在
该电子商务平台将年龄在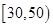 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和 的分布列与数学期望.
的分布列与数学期望.
(本小题满分12分)
在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:
(Ⅰ)若从甲、乙两名学生中选择1人参加该知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(Ⅱ)若从学生甲的6次培训成绩中随机选择2个,记选到的分数超过87分的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
在“信阳市中学生歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )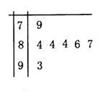
A.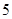 和 和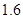 |
B. 和 和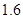 |
C. 和 和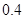 |
D.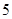 和 和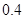 |
(本题14分)张老师居住在某城镇的A处,准备开车到学校B处上班。若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图。(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为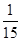 )。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量
)。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量 ,求
,求 的数学期望
的数学期望 。
。
2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:

(Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在 [8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
(本小题满分12分)在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(I)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
2015年元旦联欢晚会某师生一块做游戏,数学老师制作了六张卡片放在盒子里,卡片上分别写着六个函数:分别写着六个函数: ,
, .
.
(1)现在取两张卡片,记事件A为“所得两个函数的奇偶性相同”,求事件A的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是奇函数则停止抽取,否则继续进行,记停止时抽取次数为 ,写出
,写出 的分布列,并求其数学期望.
的分布列,并求其数学期望.
(本小题满分12分)从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示.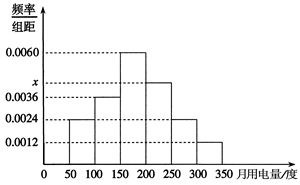
(1)根据直方图求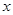 的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有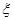 户月用电量超过300度,求
户月用电量超过300度,求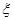 的分布列及期望.
的分布列及期望.
为了分析某篮球运动员在比赛中发挥的稳定程度,统计了该运动员在6场比赛中的得分,用茎叶图表示如图,则该组数据的方差为 .