2015年元旦联欢晚会某师生一块做游戏，数学老师制作了六张卡片放在盒子里，卡片上分别写着六个函数：分别写着六个函数：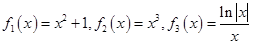
，
．
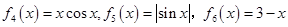（1）现在取两张卡片，记事件A为“所得两个函数的奇偶性相同”，求事件A的概率；
（2）从盒中不放回逐一抽取卡片，若取到一张卡片上的函数是奇函数则停止抽取，否则继续进行，记停止时抽取次数为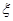
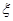，写出的分布列，并求其数学期望．
的边长为１，
，
分别为边
，
上的点．当
的周长为２时，求
的大小．
，
是
，
之间的一定点，并且
，
．
是直线
．且使
与直线
，求
面积的最小值．
，
，求
的值．
，试用含
的式子表示
．
，
，求证：
．相关知识点
推荐套卷
2015年元旦联欢晚会某师生一块做游戏，数学老师制作了六张卡片放在盒子里，卡片上分别写着六个函数：分别写着六个函数：，．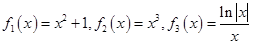
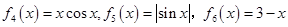（1）现在取两张卡片，记事件A为“所得两个函数的奇偶性相同”，求事件A的概率；
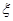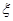（2）从盒中不放回逐一抽取卡片，若取到一张卡片上的函数是奇函数则停止抽取，否则继续进行，记停止时抽取次数为，写出的分布列，并求其数学期望．
粤公网安备 44130202000953号