贵州省贵阳市普通高中高三上学期期末监测考试理科数学试卷
设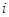 是虚数单位,复数
是虚数单位,复数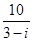 在复平面内表示的点在( )
在复平面内表示的点在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若框图所给的程序运行结果为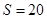 ,那么判断框中应填入的关于
,那么判断框中应填入的关于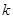 的条件是( )
的条件是( )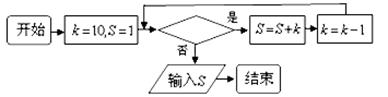
A.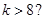 |
B.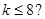 |
C.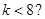 |
D.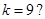 |
下列说法正确的是( )
A.命题“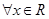 , ,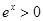 ”的否定是“ ”的否定是“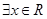 , ,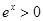 ” ” |
B.命题“已知 , ,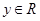 ,若 ,若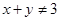 ,则 ,则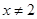 或 或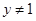 ”的逆否命题是真命题 ”的逆否命题是真命题 |
C.“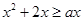 在 在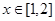 上恒成立” 上恒成立” “ “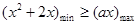 在 在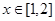 上恒成立” 上恒成立” |
D.命题“若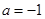 ,则函数 ,则函数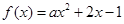 只有一个零点”的逆命题为真命题 只有一个零点”的逆命题为真命题 |
如图,点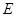 ,
,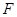 分别是正方体
分别是正方体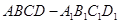 的棱
的棱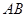 ,
,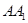 中点,点
中点,点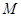 ,
,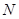 分别是线段
分别是线段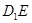 ,
,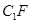 上的点,则与平面
上的点,则与平面 垂直的直线
垂直的直线 有( )条
有( )条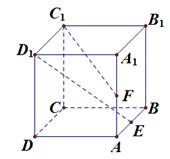
| A.0 | B.1 | C.2 | D.无穷多 |
为得到函数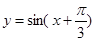 的图象,可将函数
的图象,可将函数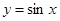 的图象向左平移
的图象向左平移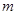 个单位长度,或向右平移
个单位长度,或向右平移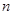 个单位长度(
个单位长度(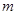 ,
,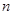 均为正整数),则
均为正整数),则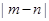 的最小值是( )
的最小值是( )
A.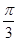 |
B.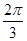 |
C.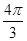 |
D.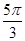 |
设双曲线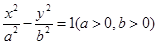 的左、右焦点分别为
的左、右焦点分别为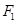 ,
,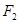 ,离心率为
,离心率为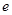 ,过
,过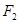 的直线与双曲线的右支交于
的直线与双曲线的右支交于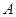 ,
,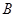 两点,若
两点,若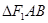 是以
是以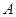 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则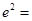 ( )
( )
A.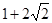 |
B.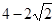 |
C.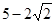 |
D.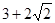 |
题文已知全集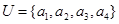 ,集合
,集合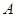 是集合
是集合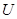 的恰有两个元素的子集,且满足下列三个条件:①若
的恰有两个元素的子集,且满足下列三个条件:①若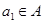 ,则
,则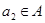 ;②若
;②若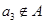 ,则
,则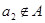 ;③若
;③若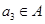 ,则
,则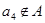 ,则集合
,则集合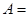 __________.(用列举法表示)
__________.(用列举法表示)
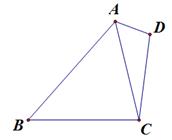
(本小题满分12分)如图所示,在四边形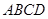 中,
中,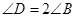 ,且
,且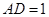 ,
,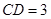 ,
,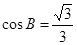 .
.
(1)求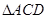 的面积;
的面积;
(2)若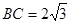 ,求
,求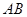 的长.
的长.
(本小题满分12分)如图,已知四棱锥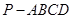 中,
中,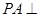 平面
平面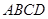 ,
,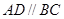 ,
,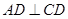 ,且
,且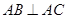 ,
,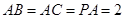 ,
,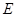 是
是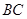 的中点.
的中点.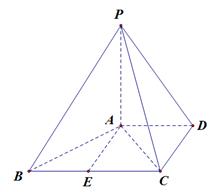
(1)求异面直线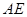 与
与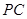 所成角;
所成角;
(2)求二面角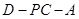 的平面角的余弦值.
的平面角的余弦值.
(本小题12分)据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
| 态度 调查人群 |
应该取消 |
应该保留 |
无所谓 |
| 在校学生 |
2100人 |
120人 |
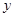 人 人 |
| 社会人士 |
600人 |
 人 人 |
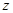 人 人 |
(1)已知在全体样本中随机抽取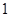 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为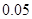 ,现用分层抽样的方法在所有参与调查的人中抽取
,现用分层抽样的方法在所有参与调查的人中抽取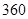 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取 人,再平均分成两组进行深入交流,求第一组中在校学生人数
人,再平均分成两组进行深入交流,求第一组中在校学生人数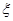 的分布列和数学期望.
的分布列和数学期望.
(本小题12分)已知椭圆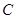 的两个焦点是
的两个焦点是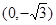 和
和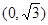 ,并且经过点
,并且经过点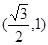 ,抛物线
,抛物线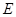 的顶点在坐标原点,焦点恰好是椭圆
的顶点在坐标原点,焦点恰好是椭圆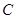 的右顶点
的右顶点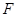 .
.
(1)求椭圆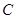 和抛物线
和抛物线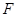 的标准方程;
的标准方程;
(2)过点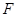 作两条斜率都存在且互相垂直的直线
作两条斜率都存在且互相垂直的直线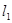 ,
,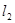 ,
,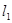 交抛物线
交抛物线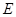 于点
于点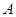 ,
,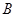 ,
,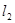 交抛物线
交抛物线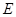 于点
于点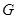 ,
,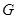 ,求
,求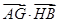 的最小值.
的最小值.
(本小题满分10分)选修4-1:平面几何选讲
如图,点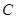 在圆
在圆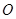 直径
直径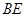 的延长线上,
的延长线上,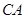 切圆
切圆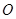 于
于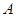 点,
点,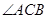 的平分线
的平分线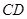 交
交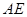 于点
于点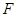 ,交
,交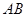 于
于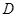 点.
点.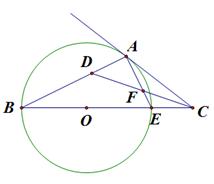
(1)求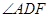 的度数;
的度数;
(2)若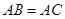 ,求
,求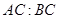 .
.
(本小题满分10分)选修4-4:极坐标于参数方程
已知曲线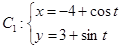 (
(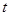 为参数),
为参数),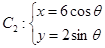 (
(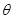 为参数).
为参数).
(1)化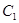 ,
,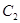 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若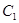 上的点
上的点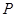 对应的参数为
对应的参数为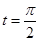 ,
,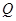 为
为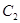 上的动点,求
上的动点,求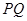 中点
中点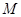 到直线
到直线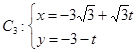 (
(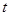 为参数)距离的最小值.
为参数)距离的最小值.
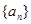 中,
中,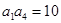 ,则数列
,则数列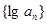 的前
的前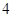 项和等于( )
项和等于( )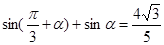 ,则
,则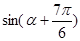 的是( )
的是( )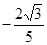
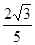
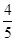
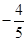
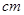 ),则该棱锥的体积是( )
),则该棱锥的体积是( )

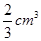
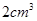
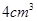
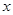 ,
,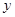 满足
满足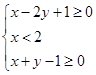 ,则
,则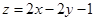 的取值范围是( )
的取值范围是( )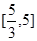
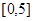
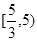
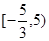
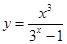 的图象大致是( )
的图象大致是( )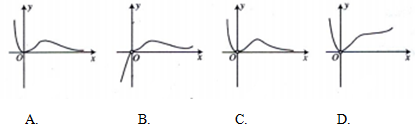
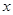 ,
,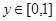 ,则点
,则点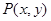 满足
满足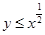 的概率为( )
的概率为( )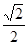
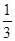
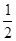
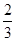
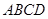 的边长为
的边长为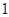 ,
,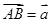 ,
,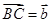 ,
,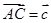 ,则
,则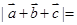 _______.
_______.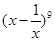 的展开式中的
的展开式中的 系数是_________(用数字作答)
系数是_________(用数字作答)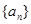 满足
满足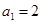 ,
,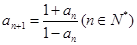 ,则该数列的前
,则该数列的前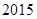 项的乘积
项的乘积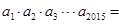 _________.
_________.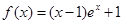 ,
,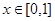 .
.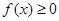 ;
;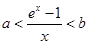 在
在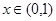 恒成立,求
恒成立,求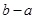 的最小值.
的最小值.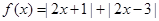 .
.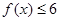 的解集;
的解集;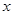 的不等式
的不等式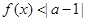 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号