高中数学随机思想的发展试题

有一批产品，其中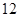件是正品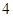，件是次品，有放回的任取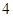件，若表示取到次品的件数，则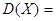                         

A．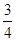

B．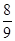

C．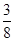

D．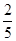

在一次运动会上，某单位派出了有6名主力队员和5名替补队员组成的代表队参加比赛.如果随机抽派5名队员上场比赛，将主力队员参加比赛的人数记为X，求随机变量X的概率分布以及随机变量X数学期望；（本题结果用分数表示即可）

一投掷飞碟的游戏中，飞碟投入红袋记2分，投入蓝袋记1分，未投入袋记0分．经过多次试验，某人投掷100个飞碟有50个入红袋，25个入蓝袋，其余不能入袋．
(1)求该人在4次投掷中恰有三次投入红袋的概率；
(2)求该人两次投掷后得分ξ的数学期望Eξ.

将编号为1、2、3、4的4个小球随机投入到编号为1、2、3、4的4个盒中，要求每盒只投1球，记球与盒编号相同的个数为 则=            .

（本小题满分12分）已知广东省某校高三（1）班有名学生,从中按照系统抽样的方法抽取名学生.
（1）若第组抽出的号码为,写出所有被抽出学生的号码；
（2）分别统计这名学生某高校自主招生考试成绩（满分:分）,获得成绩数据的茎叶图如图所示,现从这名学生中随机抽取名学生成绩,其中有名学生的成绩是超过的,求的分布列与期望.

一个袋中装有10个红球，20个白球，这些球除颜色外完全相同，一次从中摸出5个球，随机变量表示取到的红球数，服从超几何分布，则=
            （用组合数作答）

受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计数据如下：

品牌	甲	乙
首次出现故 障时间x(年)	0<x≤1	1<x≤2	x>2	0<x≤2	x>2
轿车数量(辆)	2	3	45	5	45
每辆利润 (万元)	1	2	3	1.8	2.9

将频率视为概率，解答下列问题：
(1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率．
(2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X₁，生产一辆乙品牌轿车的利润为X₂，分别求X₁，X₂的分布列．
(3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．

我市在夜明珠与黄柏河交汇形成的平湖水面上修建”三峡游轮中心”．其中有小型游艇出租给游客游玩，收费标准如下：租用时间不超过2小时收费100，超过2小时的部分按每小时100收取（不足一小时按一小时计算）．现甲、乙两人独立来该景点租用小型游艇，各租一次．设甲、乙租用不超过两小时的概率分别为，；租用2小时以上且不超过3小时的概率分别为，，且两人租用的时间都不超过4小时．
（Ⅰ）求甲、乙两人所付费用相同的概率；
（Ⅱ）设甲、乙两人所付的费用之和为随机变量，求的分布列与数学期望．

（本小题满分12分）某地宫有三个通道，进入地宫的每个人都要经过一扇智能门。首次到达此门，系统会随机（即等可能）为你打开一个通道，若是1号通道，则需要1小时走出地宫；若是2号、3号通道，则分别需要2小时、3小时返回智能门。再次到达智能门时，系统会随机打开一个你未到过的通道，直至走完地宫为止。令表示走出地宫所需的时间。
（1）求的分布列； 
（2）求的数学期望。

已知随机变量，若～，则分别是（ ）

A．6和2.4

B．2和2.4

C．2和5.6

D．6和5.6

某超市有奖促销，抽奖规则是：每消费满50元，即可抽奖一次.抽奖方法是：在不透明的盒内装有标着1，2，3，4，5号码的5个小球，从中任取1球，若号码大于3就奖励10元，否则无奖，之后将球放回盒中，即完成一次抽奖，则某人抽奖2次恰中20元的概率为___________；若某人消费200元，则他中奖金额的期望是_________元.

某市有一个玉米种植基地．该基地的技术员通过种植实验发现，一种品质优良的玉米种子每粒发芽的概率都为0．95，现在该种植基地播种了10000粒这种玉米种子，对于没有发芽的种子，每粒需再播种1粒，补种的种子数记为，则的数学期望    ．

（本小题满分12分）深圳市于2014年12月29日起实施小汽车限购政策．根据规定，每年发放10万个小汽车名额，其中电动小汽车占20%，通过摇号方式发放，其余名额通过摇号和竞价两种方式各发放一半．政策推出后，某网站针对不同年龄段的申请意向进行了调查，结果如下表所示：

申请意向 年龄	摇号	竞价（人数）	合计
电动小汽车（人数）	非电动小汽车（人数）
30岁以下 （含30岁）	50	100	50	200
30至50岁 （含50岁）	50	150	300	500
50岁以上	100	150	50	300
合计	200	400	400	1000

 
（1）采取分层抽样的方式从30至50岁的人中抽取10人，求其中各种意向人数；
（2）在（1）中选出的10个人中随机抽取4人，求其中恰有2人有竞价申请意向的概率；
（3）用样本估计总体，在全体市民中任意选取4人，其中摇号申请电动小汽车意向的人数记为，求的分布列和数学期望．

已知离散型随机变量X的分布列如表，若E(X)＝0，D(X)＝1，则a＝________，b＝________.

X	－1	0	1	2
P	a	b	c

2011年深圳大运会，某运动项目设置了难度不同的甲、乙两个系列，每个系列都有K和D两个动作，比赛时每位运动员自选一个系列完成，两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的，根据赛前训练统计数据，某运动员完成甲系列和乙系列的情况如下表：
甲系列：

动作	K	D
得分	100	80	40	10
概率

乙系列：

动作	K	D
得分	90	50	20	0
概率

   现该运动员最后一个出场，其之前运动员的最高得分为118分。
（I）若该运动员希望获得该项目的第一名，应选择哪个系列，说明理由，并求其获得第一名的概率；
（II）若该运动员选择乙系列，求其成绩X的分布列及其数学期望EX