高中数学随机思想的发展试题

（本题满分分） 某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验．选取两大块地，每大块地分成n小块地，在总共2n小块地中，随机选n小块地种植品种甲，另外n小块地种植品种乙．
（I）假设n=2，求第一大块地都种植品种甲的概率；
（II）试验时每大块地分成8小块，即n=8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量（单位：kg/hm²）如下表：

品种甲	403	397	390	404	388	400	412	406
品种乙	419	403	412	418	408	423	400	413

分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？
附：样本数据的的样本方差，其中为样本平均数．

设随机变量X的分布列如下：

X	0	5	10	20
P	0.1	α	β	0.2

若数学期望，则方差       ．

（本小题共13分）某市医疗保险实行定点医疗制度，按照“就近就医、方便管理”的原则，参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构．若甲、乙、丙、丁4名参加保险人员所在地区附近有A，B，C三家社区医院，并且他们的选择是相互独立的．
（Ⅰ）求甲、乙两人都选择A社区医院的概率；
（Ⅱ）求甲、乙两人不选择同一家社区医院的概率；
（Ⅲ）设4名参加保险人员中选择A社区医院的人数为ξ，求ξ的分布列和数学期望．

2011年3月20日，第19个世界水日，主题是：“城市水资源管理”；2011年“六·五”世界环境日中国主题：“共建生态文明，共享绿色未来”．活动组织者为调查市民对活动主题的了解情况，随机对10～60岁的人群抽查了人，调查的每个人都同时回答了两个问题，统计结果如下：

（Ⅰ）若以表中的频率近似看作各年龄段回答活动主题正确的概率，规定回答正确世界环境日中国主题的得20元奖励，回答正确世界水日主题的得30元奖励．组织者随机请一个家庭中的两名成员（大人42岁，孩子16岁）回答这两个主题，两个主题能否回答正确均无影响，分别写出这个家庭两个成员获得奖励的分布列并求该家庭获得奖励的期望；
（Ⅱ）求该家庭获得奖励为50元的概率．

同室4人各写1张贺年卡，先集中起来，然后每人从中各拿1张贺年卡，记取回自己贺年卡的同学个数为，则的数学期望为      

某商场为吸引顾客消费推出一项优惠活动.活动规则如下：消费额每满100元可转动如图所示的圆盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置. 若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券. 例如：消费218元，可转动圆盘2次，所获得的返券金额是两次金额之和.
（1）若某位顾客消费128元，求返券金额不低于30元的概率；
（2）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记
为（元）.求随机变量的分布列和数学期望.

（本小题满分12分）
将10个白小球中的3个染成红色，3个染成黄色，试解决下列问题：
求取出3个小球中红球个数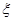的分布列和数学期望；
求取出3个小球中红球个数多于白球个数的概率.

在一次抗洪抢险中准备用射击的方法引爆从上游漂流而下的一个巨大汽油罐。已知只有5发子弹，第一次命中只能使汽油流出，第二次命中才能引爆。每次射击是相互独立的，且命中的概率都是。
(1)求油罐被引爆的概率；
(2)如果引爆或子弹打光停止射击，设射击次数为，求的分布列及数学期望。

为振兴旅游业，四川省2009年面向国内发行总量为2000万张的熊猫优惠卡，向省外人士发行的是熊猫金卡（简称金卡），向省内人士发行的是熊猫银卡（简称银卡）。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游，其中是省外游客，其余是省内游客。在省外游客中有持金卡，在省内游客中有持银卡。
（I）在该团中随机采访3名游客，求恰有1人持金卡且持银卡者少于2人的概率；
（II）在该团的省内游客中随机采访3名游客，设其中持银卡人数为随机变量，
求的分布列及数学期望。

（本小题满分12分）
某象棋教练用下列方式考核队员:任一名队员可以选择与一级棋士或二级棋士对奕,规定与一级棋士对奕取胜得3分,不胜得0分,与二级棋士对弈取胜得2分,不胜得0分,如果前两局得分超过3分即算考核合格,否则比赛三局.某位队员与一级棋士对弈获胜的概率为q₁,与二级棋士对弈获胜的概率为0.6,该队员选择先与一级棋士对奕,以后都与二级棋士对奕,用X表示该队员考核结束后所得的总分,已知P(X=0)=0.128.
(1)求q₁的值;
(2)写出随机变量X的分布列并求出数学期望EX;
(3)试比较该队员选择都与二级棋士对奕与上述方式最后得分大于3的概率的大小;

（本小题满分12分）
2009年高考,本市一高中预计有6人达到清华大学(或北京大学)的录取分数线,为此,市体彩中心拟对其中的三位家庭较困难学生进行资助,现由体彩中心的两位负责人独立地对这三位学生的家庭情况进行考察,假设考察结果为"资助"与"不资助"的概率都是,若某位学生获得两个"资助",则一次给予5万元的助学资金;若获得一个"资助",则一次性给予2万元的助学资金;若未获得"资助",则不予资助;若用X表示体彩中心的资助总额.
(1)写出随机变量X的分布列;(2)求数学期望EX;

(本小题满分12分)
甲、乙、丙3人投篮，投进的概率分别是
（I）若3人各投篮1次,求3人都没有投进的概率;
（Ⅱ）（文）若3人各投篮1次,求3人恰有一人投进的概率
（理）用表示乙投篮3次的进球数,求随机变量的概率分布及数学期望.

有编号为的个学生，入坐编号为的个座位．每个学生规定坐一个座位，设学生所坐的座位号与该生的编号不同的学生人数为，已知时，共有种坐法．
（1）求的值；
（2）求随机变量的概率分布列和数学期望．

设随机变量ξ～N(μ，σ² )，且 P(ξ)= P(ξ)，则c ="(  " )（  C  ）

A．σ^2

B．σ

C．μ

D．–μ

（本小题满分12分）
一个口袋巾装有标号为1，2，3的6个小球，其中标号1的小球有1个，标号2的小球有2个，标号3的小球有3个，现从口袋中随机摸出2个小球．
（I）求摸出2个小球标号之和为3的概率；
（II）求摸出2个小球标号之和为偶数的概率；
（III）用表示摸出2个小球的标号之和，写出的分布列，并求的数学期望．