[北京]2012届北京市丰台区高三上学期期末考试理科数学
已知命题p: ,
, ,命题q:
,命题q: ,
, ,则( )
,则( )
A.命题 是假命题 是假命题 |
B.命题 是真命题 是真命题 |
C.命题 是假命题 是假命题 |
D.命题 是真命题 是真命题 |
预测人口的变化趋势有多种方法,“直接推算法”使用的公式是 ,其中Pn为预测人口数,P0为初期人口数,k为预测年内增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么这期间人口数 ( )
,其中Pn为预测人口数,P0为初期人口数,k为预测年内增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么这期间人口数 ( )
| A.呈上升趋势 | B.呈下降趋势 | C.摆动变化 | D.不变 |
如图,P是正方体ABCD—A1B1C1D1对角线AC1上一动点,设AP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )
 (A) |
 (B) |
 (C) |
 (D) |

函数 的导函数为
的导函数为 ,若对于定义域内任意
,若对于定义域内任意 ,
,
 ,有
,有 恒成立,则称
恒成立,则称 为恒均变函数.给出下列函数:①
为恒均变函数.给出下列函数:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
.其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
(本小题共14分)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2, ,CC1=4,M是棱CC1上一点.
,CC1=4,M是棱CC1上一点.
(Ⅰ)求证:BC⊥AM;
(Ⅱ)若M,N分别是CC1,AB的中点,求证:CN //平面AB1M;
(Ⅲ)若 ,求二面角A-MB1-C的大小.
,求二面角A-MB1-C的大小.
(本小题共13分)某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有A,B,C三家社区医院,并且他们的选择是相互独立的.
(Ⅰ)求甲、乙两人都选择A社区医院的概率;
(Ⅱ)求甲、乙两人不选择同一家社区医院的概率;
(Ⅲ)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
.(本小题共13分)在平面直角坐标系xOy中, 为坐标原点,动点
为坐标原点,动点 与两个定点
与两个定点 ,
, 的距离之比为
的距离之比为 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)若直线 :
: 与曲线
与曲线 交于
交于 ,
, 两点,在曲线
两点,在曲线 上是否存在一点
上是否存在一点 ,使得
,使得 ,若存在,求出此时直线
,若存在,求出此时直线 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.
(本小题共14分)设函数 在
在 处取得极值.
处取得极值.
(Ⅰ)求 与
与 满足的关系式;
满足的关系式;
(Ⅱ)若 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若 ,函数
,函数 ,若存在
,若存在 ,
, ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
 ,则( )
,则( ) B
B

 对应的点位于( )
对应的点位于( )







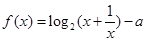 在区间
在区间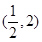 内有零点,则实数a的取值范围是( )
内有零点,则实数a的取值范围是( )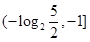
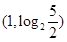

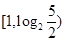
 ,
, ,则
,则 与
与 的夹角余弦值等于
的夹角余弦值等于 的概率是
的概率是 .
. 的最小正周期和值域;
的最小正周期和值域; 为第二象限角,且
为第二象限角,且 ,求
,求 的值.
的值. ,且
,且 ,求m的最小值.
,求m的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号