有编号为 的
的 个学生,入坐编号为
个学生,入坐编号为 的
的 个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为 ,已知
,已知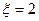 时,共有
时,共有 种坐法.
种坐法.
(1)求 的值;
的值;
(2)求随机变量 的概率分布列和数学期望.
的概率分布列和数学期望.
相关知识点
推荐套卷
有编号为 的
的 个学生,入坐编号为
个学生,入坐编号为 的
的 个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为 ,已知
,已知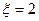 时,共有
时,共有 种坐法.
种坐法.
(1)求 的值;
的值;
(2)求随机变量 的概率分布列和数学期望.
的概率分布列和数学期望.