某大型工厂的车床有甲,乙,丙三个型号,分别占总数的 ,
,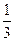 ,
,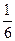 ,现在有三名工人各自独立选一台车床操作.
,现在有三名工人各自独立选一台车床操作.
(I)求他们选择的车床类型互不相同的概率;
(II)设ξ为他们选择甲型或丙型车床的人数,求ξ的分布列及数学期望.
(12分)某电视台综艺频道主办一种有奖过关游戏,该游戏设有两关,只有过了第一关,才能玩第二关,每关最多玩两次,连续两次失败者被淘汰出局.过关者可获奖金,只过第一关获奖金900元,两关全过获奖金3600元.某同学有幸参与了上述游戏,且该同学每一次过关的概率均为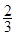 ,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
(1)求该同学仅获得900元奖金的概率;
(2)若该同学已顺利通过第一关,求他获得3600元奖金的概率;
(3)求该同学获得奖金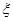 的数学期望(精确到元).
的数学期望(精确到元).
有专业机构认为甲型N1H1流感在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过15人” .根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
| A.甲地:总体均值为6,中位数为8 |
| B.乙地: 总体均值为5,总体方差为12 |
| C.丙地:中位数为5,众数为6 |
| D.丁地:总体均值为3,总体方差大于0 |
(本小题满分10分)2010年3月国家要求一些企业必须停业处理排污问题,于是各企业考虑引进污水处理设备,现有甲、乙两套设备可以引进。每个企业可引进一套,引进两套或都不引进自行研发。对于每个企业,甲被引进的概率为 ,乙被引进的概率为
,乙被引进的概率为 ,甲乙两套设备是否被引进相互独立,各企业之间是否引进也是相互独立的。
,甲乙两套设备是否被引进相互独立,各企业之间是否引进也是相互独立的。
(Ⅰ)求A企业引进污水处理设备的概率;
(Ⅱ)记X表示3个企业中引进污水处理设备的企业个数,求X的分布列及期望。
甲乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下,
甲运动员 乙运动员
| 射击环数 |
频数 |
频率 |
| 7 |
8 |
0.1 |
| 8 |
12 |
0.15 |
| 9 |
Z |
|
| 10 |
|
0.35 |
| 合计 |
80 |
1 |
| 射击环数 |
频数 |
频率 |
| 7 |
10 |
0.1 |
| 8 |
10 |
0.1 |
| 9 |
X |
0.45 |
| 10 |
35 |
Y |
| 合计 |
100 |
1 |
若将频率视为概率,回答下列问题,
(1) 求甲运动员击中10环的概率;
(2) 求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率;
(3) 若甲运动员射击2次,乙运动员射击1次, 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求 的分布列以及
的分布列以及 。
。
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(1)求这箱产品被用户接收的概率;
(2)记抽检的产品件数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
某商场买来一车苹果,从中随机抽取了10个苹果,其重量(单位:克)分别为:150,152,153,149,148,146,151,150,152,147,由此估计这车苹果单个重量的期望值是( )
| A.150.2克 | B.149.8克 | C.149.4克 | D.147.8克 |
| 付款方式 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
| 频 数 |
40 |
20 |
 |
10 |
 |
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如右表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元. 用 表示经销一辆汽车的利润.(1)求上表中的
表示经销一辆汽车的利润.(1)求上表中的 值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率 ;(3)求
;(3)求 的分布列及数学期望
的分布列及数学期望 .
.
(本小题满分12分)某公司为庆祝元旦举办了一个抽奖活动,现场准备的抽奖箱里放置了分别标有数字1000、800﹑600、0的四个球(球的大小相同).参与者随机从抽奖箱里摸取一球(取后即放回),公司即赠送与此球上所标数字等额的奖金(元),并规定摸到标有数字0的球时可以再摸一次﹐但是所得奖金减半(若再摸到标有数字0的球就没有第三次摸球机会),求一个参与抽奖活动的人可得奖金的期望值是多少元.
(本小题满分12分)
全球金融危机,波及中国股市,甲、乙、丙、丁四人打算趁目前股市低迷之际“抄底”,若四人商定在圈定的6只股票中各自随机购买一只(假定购买时每支股票的基本情况完全相同).
(1)求甲、乙、丙、丁四人恰好买到同一只股票的概率;
(2)求甲、乙、丙、丁四人中至多有两人买到同一只股票的概率;
(3)由于中国政府采取了积极的应对措施,股市渐趋“回暖”.若某人今天按上一交易日的收盘价20元/股,买入某只股票1000股,且预计今天收盘时,该只股票比上一交易日的收盘价上涨10%(涨停)的概率为0.6.持平的概率为0.2,否则将下跌10%(跌停),求此人今天获利的数学期望(不考虑佣金、印花税等交易费用).
一个盒子装有六张卡片,上面分别写着如下六个定义域为 的函数:
的函数: ,
, ,
, ,
, ,
, ,
, .
.
(Ⅰ)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(Ⅱ)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数 的分布列和数学期望.
的分布列和数学期望.