(12分)某电视台综艺频道主办一种有奖过关游戏,该游戏设有两关,只有过了第一关,才能玩第二关,每关最多玩两次,连续两次失败者被淘汰出局.过关者可获奖金,只过第一关获奖金900元,两关全过获奖金3600元.某同学有幸参与了上述游戏,且该同学每一次过关的概率均为 ,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
(1)求该同学仅获得900元奖金的概率;
(2)若该同学已顺利通过第一关,求他获得3600元奖金的概率;
(3)求该同学获得奖金 的数学期望(精确到元).
的数学期望(精确到元).
相关知识点
推荐套卷
 :
: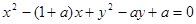 .
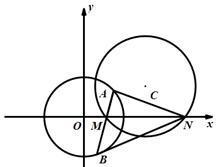
.
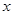 轴相切,求圆
轴相切,求圆 ,圆C与
,圆C与 (点
(点 在点
在点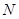 的左侧).过点
的左侧).过点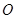 :
: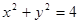 相交于两点
相交于两点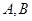 .问:是否存在实数
.问:是否存在实数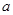 ,使得
,使得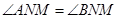 ?若存在,求出实数
?若存在,求出实数 ,底面
,底面 是平行四边形,点
是平行四边形,点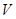 在平面
在平面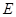 在
在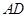 边上,且
边上,且 ,
,
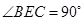 .
.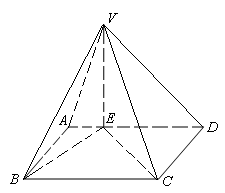
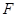 是
是 的中点,求异面直线
的中点,求异面直线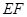 与
与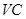 所成角的余弦值;
所成角的余弦值;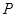 在棱
在棱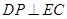 .求
.求 的值.
的值.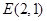 和圆
和圆 :
: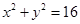 .
.
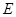 的直线
的直线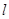 被圆
被圆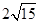 ,求直线
,求直线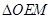 的面积
的面积 ,且
,且 是圆
是圆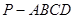 中,底面
中,底面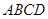 是直角梯形,
是直角梯形,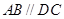 ,
,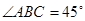 ,
, ,
,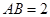 ,
,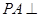 平面
平面 .
.
 平面
平面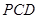 ;
; 平面
平面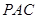 ;
; 是
是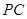 的中点,求三棱锥
的中点,求三棱锥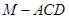 的体积.
的体积.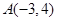 点射出,到
点射出,到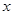 轴上的
轴上的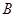 点后,被
点后,被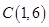 ,求
,求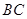 所在直线的方程及点
所在直线的方程及点 粤公网安备 44130202000953号
粤公网安备 44130202000953号