某大楼共5层,4个人从第一层上电梯,假设每个人都等可能地在每一层下电梯,并且他们下电梯与否相互独立. 又知电梯只在有人下时才停止.
(Ⅰ)求某乘客在第 层下电梯的概率
层下电梯的概率 ;
;
(Ⅱ)求电梯在第2层停下的概率;
(Ⅲ)求电梯停下的次数 的数学期望.
的数学期望.
已知随机变量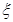 的分布列如下表所示,
的分布列如下表所示,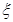 的期望
的期望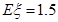 ,则
,则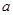 的值等于;
的值等于;
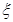 |
0 |
1 |
2 |
3 |
| P |
0.1 |
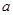 |
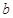 |
0.2 |
已知随机变量X的分布列为P(X =k)=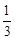 ,k=1,2,3,则D(3X +5)等于 ()
,k=1,2,3,则D(3X +5)等于 ()
| A.6 | B.9 | C.3 | D.4 |
有5支竹签,编号分别为1,2,3,4,5,从中任取3支,以X表示取出竹签的最大号码,则EX的值为( )
| A.4 | B.4.5 | C.4.75 | D.5 |
随机抽取某厂的某种产品200件,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而生产1件次品亏损2万元,设一件产品获得的利润为X(单位:万元).
(1)求X的分布列;
(2)求1件产品的平均利润(即X的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求生产1件产品获得的平均利润不小于4.73万元,则三等品率最多是多少?
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 和
和 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数 的分布列与期望.
的分布列与期望.
在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(Ⅰ)摸出的3个球为白球的概率是多少?
(Ⅱ)摸出的3个球为2个黄球1个白球的概率是多少?
(III)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
某大学自主招生面试时将20名学生平均分成甲,乙两组,其中甲组有4名女学生,乙组有6名女学生.现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名学生进行第一轮面试.
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的学生中恰有1名女学生的概率;
(Ⅲ)求抽取的4名学生中恰有2名男学生的概率.
某校为了解高一年级学生身高情况,按10%的比例对全校700名高一学生按性别进行抽样检查,测得身高频数分布表如下:
表1:男生身高频数分布表
| 身高(cm) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
[180,185) |
[185,190) |
| 频数 |
2 |
5 |
13 |
13 |
5 |
2 |
表2:女生身高频数分布表
| 身高(cm) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
| 频数 |
1 |
8 |
12 |
5 |
3 |
1 |
(Ⅰ)求该校高一男生的人数;
(Ⅱ)估计该校高一学生身高(单位:cm)在[165,180)的概率;
(Ⅲ)在男生样本中,从身高(单位:cm)在[180,190)的男生中任选3人,设ξ表示所选3人中身高(单位:cm)在[180,185)的人数,求ξ的分布列和数学期望.
| ξ |
1 |
2 |
3 |
 |
 |
 |
 |
甲、乙、丙三人分别独立地解一道题,甲做对的概率是 ,三人都做对的概率是
,三人都做对的概率是 ,三人全做错的概率是
,三人全做错的概率是 ,已知乙做对这道题的概率大于丙做对这道题的概率.设三人中做对这道题的人数为
,已知乙做对这道题的概率大于丙做对这道题的概率.设三人中做对这道题的人数为 ,则随机变量
,则随机变量 的数学期望
的数学期望 .
.
(本小题满分10分)
某电子科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自独立进行为期一个月的技术攻关,同时决定对攻关限期内攻克技术难题的小组给予奖励. 已知此技术难题在攻关期限内被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 ,
,
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及数学期望
的分布列及数学期望 ;
;
(2)设 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递增”为事件C,求事件C发生的概率;
在定义域内单调递增”为事件C,求事件C发生的概率;