(10分)在一次国际大型体育运动会上，某运动员报名参加了其中5个项目的比赛．已知该运动员在这5个项目中，每个项目能打破世界纪录的概率都是0.8，那么在本次运动会上：
（1）求该运动员至少能打破3项世界纪录的概率；
（2）若该运动员能打破世界纪录的项目数为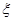
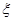，求的数学期望
（即均值）．
相关试题
.
的最小正周期和最值；
.
时，求
处的切线方程；
时，
，求
的取值范围.
，其中
，若函数
，且函数
的图象与直线
相邻两公共点间的距离为
.
的值；
中．
分别是
的对边，且
，求
.
，求
的值；
的单调递增区间.
，若
且对任意实数
均有
成立.
表达式；
是单调函数，求实数
的取值范围.相关知识点
推荐套卷
(10分)在一次国际大型体育运动会上，某运动员报名参加了其中5个项目的比赛．已知该运动员在这5个项目中，每个项目能打破世界纪录的概率都是0.8，那么在本次运动会上：
（1）求该运动员至少能打破3项世界纪录的概率；
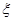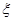（2）若该运动员能打破世界纪录的项目数为，求的数学期望（即均值）．
粤公网安备 44130202000953号