如图，已知椭圆
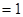（a＞b＞0）的离心率
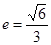，过顶点A、B的直线与原点的距离为
．
（1）求椭圆的方程．
（2）已知定点E（-1，0），若直线y＝kx＋2（k≠0）与椭圆交于C、D两点．问：是否存在k的值，使以CD为直径的圆过E点?请说明理由．
；
=
＋
．
,当实数
取何值时,
＋2
与2
=(-1,x)与
="(-x," 2)共线且方向相同，求x推荐套卷
如图，已知椭圆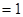（a＞b＞0）的离心率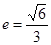，过顶点A、B的直线与原点的距离为．
（1）求椭圆的方程．
（2）已知定点E（-1，0），若直线y＝kx＋2（k≠0）与椭圆交于C、D两点．问：是否存在k的值，使以CD为直径的圆过E点?请说明理由．
粤公网安备 44130202000953号