抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:
则成绩较稳定(方差较小)的那位运动员成绩的方差为.
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
①求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
2013年4月20日8时02分四川省雅安市芦山县(北纬30.3,东经103.0)发生7.0级地震。一方有难,八方支援,重庆众多医务工作者和志愿者加入了抗灾救援行动。其中重庆某医院外科派出由5名骨干医生组成的救援小组,奔赴受灾第一线参与救援。现将这5名医生分别随机分配到受灾最严重的芦山、宝山、天全三县中的某一个。
(1)求每个县至少分配到一名医生的概率。
(2)若将随机分配到芦山县的人数记为 ,求随机变量
,求随机变量 的分布列,期望和方差。
的分布列,期望和方差。
甲、乙两个同学同时报名参加某重点高校2010年自主招生,高考前自主招生的程序为审核材料和文化测试,只有审核过关后才能参加文化测试,文化测试合格者即可获得自主招生入选资格。已知甲,乙两人审核过关的概率分别为 ,审核过关后,甲、乙两人文化测试合格的概率分别为
,审核过关后,甲、乙两人文化测试合格的概率分别为
(1)求甲,乙两人至少有一人通过审核的概率;
(2)设 表示甲,乙两人中获得自主招生入选资格的人数,求
表示甲,乙两人中获得自主招生入选资格的人数,求 的数学期望.
的数学期望.
在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用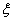 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。
(Ⅰ)写出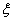 的分布列;(以列表的形式给出结论,不必写计算过程)
的分布列;(以列表的形式给出结论,不必写计算过程)
(Ⅱ)求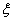 的数学期望
的数学期望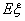 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理)
某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
7 |
7 |
8 |
7 |
| 乙班 |
6 |
7 |
6 |
7 |
9 |
则以上两组数据的方差中较小的一个为 =.
=.
抽签方式决定出场顺序.通过预赛,选拔出甲、乙等五支队伍参加决赛.
(Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率;
(Ⅱ)若决赛中甲队和乙队之间间隔的队伍数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
2012年3月2日,江苏卫视推出全新益智答题类节目《一站到底》,甲、乙两人报名参加《一站到底》面试的初试选拔,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次抢答都从备选题中随机抽出3题进行测试,至少答对2题初试才能通过.
(Ⅰ)求甲答对试题数ξ的概率分布及数学期望;
(Ⅱ)求甲、乙两人至少有一人初试通过的概率.
在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各 有六位同学选择科目甲或科 目乙,情况如下表:
| 科目甲 |
科目乙 |
总计 |
|
| 第一小组 |
1 |
5 |
6 |
| 第二小组 |
2 |
4 |
6 |
| 总计 |
3 |
9 |
12 |
现从第一小组、第二小 组中各任选2人分析选课情况.
(1)求选出的4 人均选科目乙的概率;
(2)设 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求 的分布列和数学期望.
的分布列和数学期望.
某人从标有1、2、3、4的四张卡片中任意抽取两张.约定如下:如果出现两个偶数或两个奇数,就将两数相加的和记为 ;如果出现一奇一偶,则将它们的差的绝对值记为
;如果出现一奇一偶,则将它们的差的绝对值记为 ,则随机变量
,则随机变量 的数学期望为.
的数学期望为.
某品牌汽车4S店对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:
| 付款方式 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
| 频数 |
40 |
20 |
 |
10 |
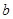 |
已知分3期付款的频率为0.2,4s店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元,分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润。
(Ⅰ)求上表中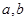 的值;
的值;
(Ⅱ)若以频率作为概率,求事件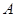 :“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率 ;
;
(Ⅲ)求Y的分布列及数学期望EY.
在平面 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
.
(1)定义横、纵坐标为整数的点为“整点”. 在区域 中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域
中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域 中的概率;
中的概率;
(2)在区域 中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域
中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域 中的个数为
中的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
某中学校本课程共开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:
(1)求这3名学生选修课所有选法的总数;
(2)求恰有2门选修课没有被这3名学生选择的概率;
(3)求A选修课被这3名学生选择的人数的数学期望.