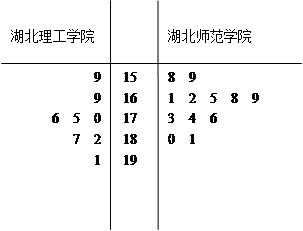袋子 和
和 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从 中摸一个红球的概率是
中摸一个红球的概率是 ,从
,从 中摸出一个红球的概率为
中摸出一个红球的概率为 .
.
⑴从A中有放回地摸球,每次摸出一个,有3次摸到红球则停止.
① 求恰好摸5次停止的概率;
② 记5次之内(含5次)摸到红球的次数为 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
⑵若A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是 ,求
,求 的值.
的值.
一个盒子里装有相同大小的黑球10个,红球12个,白球4个.从中任取两个,其中白球的个数记为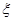 ,则下列算式中等于
,则下列算式中等于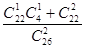 的是( )
的是( )
A.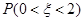 |
B.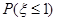 |
C.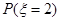 |
D.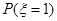 |
某次考试共有8道选择题,每道选择题有四个选项,只有一道是正确的,评分标准为:“选对得5分,不选或选错得0分。”某考生已确定有5道题的答案是正确的,其余3道题中,有一道题可以判断出两个选项是错误的,有一道题可以判断出一个选项是错误的,还有一道是乱猜的,试求该考生
(1)得40分的概率;
(2)所得分数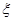 的分布及期望.
的分布及期望.
在三次独立重复试验中,事件A在每次试验中发生的概率相同,若事件A至少发生一次的概率为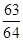 ,则事件A恰好发生一次的概率为( )
,则事件A恰好发生一次的概率为( )
A.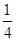 |
B.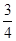 |
C.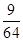 |
D.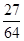 |
设随机变量 服从分布B(n,p),且E
服从分布B(n,p),且E =1.6,D
=1.6,D =1.28则( )
=1.28则( )
| A.n=4,p="0.4" | B.n=5,p=0.32 | C.n=8,p=0.2 | D.n=7,p=0.45 |
某电视台有A、B两种智力闯关游戏,甲、乙、丙、丁四人参加,其中甲乙两人各自独立进行游戏A,丙丁两人各自独立进行游戏B.已知甲、乙两人各自闯关成功的概率均为 ,丙、丁两人各自闯关成功的概率均为
,丙、丁两人各自闯关成功的概率均为 .
.
(I )求游戏A被闯关成功的人数多于游戏B被闯关成功的人数的概率;
(II) 记游戏A、B被闯关成功的总人数为 ,求
,求 的分布列和期望.
的分布列和期望.
北京的高考数学试卷中共有8道选择题,每个选择题都给了4个选项(其中有且仅有一个选项是正确的).评分标准规定:每题只选1项,答对得5分,不答或答错得0分.某考生每道题都给出了答案,已确定有4道题的答案是正确的,而其余的题中,有两道题每题都可判断其有两个选项是错误的,有一道题可以判断其一个选项是错误的,还有一道题因不理解题意只能乱猜.对于这8道选择题,试求:
(Ⅰ) 该考生得分为40分的概率;
(Ⅱ) 该考生所得分数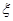 的分布列及数学期望
的分布列及数学期望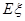 .
.
在四次独立重复试验中,随机事件A恰好发生1次的概率不大于其恰好发生两次的概率,则事件A在一次试验中发生的概率P的取值范围是( )
A. |
B.[0,0.6] | C.(0,0. 4] | D.[0.6,1) |
已知随机变量ξ的概率分布如下:
| ξ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| P |
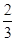 |
 |
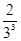 |
 |
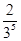 |
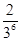 |
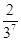 |
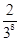 |
 |
m |
则P(ξ=10)等于( )
A、 B、
B、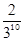 C、
C、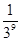 D.、
D.、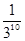
在三次独立重复试验中,事件A在每次试验中发生的概率相同,若事件A至少发生一次的概率为 ,则事件A恰好发生一次的概率为( )
,则事件A恰好发生一次的概率为( )
A. |
B. |
C. |
D. |
六名学生需依次进行身体体能和外语两个项目的训练及考核。每个项目只有一次补考机会,补考不合格者不能进入下一个项目的训练(即淘汰),若每个学生身体体能考核合格的概率是 ,外语考核合格的概率是
,外语考核合格的概率是 ,假设每一次考试是否合格互不影响。
,假设每一次考试是否合格互不影响。
①求某个学生不被淘汰的概率。
②求6名学生至多有两名被淘汰的概率
③假设某学生不放弃每一次考核的机会,用 表示其参加补考的次数,求随机变量
表示其参加补考的次数,求随机变量 的概率。
的概率。
中国 黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有湖北师范学院的“高个子”才能担任“兼职导游”。
(1)根据志愿者的身高编茎叶图指出湖北师范学院志愿者身高的中位数;
(2)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(3)若从所有“高个子”中选3名志愿者,用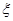 表示所选志愿者中能担任“兼职导游”的人数,试写出
表示所选志愿者中能担任“兼职导游”的人数,试写出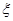 的分布列,并求
的分布列,并求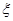 的数学期望。
的数学期望。