北京的高考数学试卷中共有8道选择题,每个选择题都给了4个选项(其中有且仅有一个选项是正确的).评分标准规定:每题只选1项,答对得5分,不答或答错得0分.某考生每道题都给出了答案,已确定有4道题的答案是正确的,而其余的题中,有两道题每题都可判断其有两个选项是错误的,有一道题可以判断其一个选项是错误的,还有一道题因不理解题意只能乱猜.对于这8道选择题,试求:
(Ⅰ) 该考生得分为40分的概率;
(Ⅱ) 该考生所得分数 的分布列及数学期望
的分布列及数学期望 .
.
相关知识点
推荐套卷
 ,求
,求 的值;
的值; 为第二象限角,化简
为第二象限角,化简
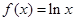 ,
,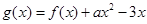 ,函数
,函数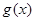 的图像在点
的图像在点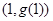 处的切线平行于
处的切线平行于 轴.
轴. 的值;
的值;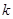 的直线与函数
的直线与函数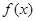 的图象交于两点
的图象交于两点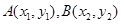 ,(
,( )
) .
.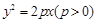 的焦点为
的焦点为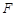 ,点
,点 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4, .
.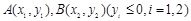 是抛物线上的两点,
是抛物线上的两点, 的角平分线与
的角平分线与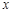 轴垂直,求直线AB的斜率;
轴垂直,求直线AB的斜率;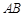 过点
过点 ,求弦
,求弦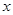 与身高
与身高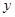 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为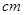 )作为样本如下表所示.
)作为样本如下表所示.
 ;
; ,试估计此人的身高;
,试估计此人的身高;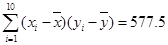 ,
,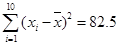 ,
,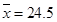 ,
,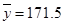 )
)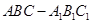 中,侧棱
中,侧棱 底面
底面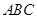 ,
,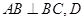 为
为 的中点,
的中点,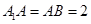 ,
,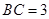 .
.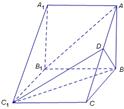
 平面
平面 ;
;  的体积.
的体积. 粤公网安备 44130202000953号
粤公网安备 44130202000953号