某电视台有A、B两种智力闯关游戏,甲、乙、丙、丁四人参加,其中甲乙两人各自独立进行游戏A,丙丁两人各自独立进行游戏B.已知甲、乙两人各自闯关成功的概率均为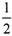 ,丙、丁两人各自闯关成功的概率均为
,丙、丁两人各自闯关成功的概率均为 .
.
(I )求游戏A被闯关成功的人数多于游戏B被闯关成功的人数的概率;
(II) 记游戏A、B被闯关成功的总人数为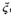 ,求
,求 的分布列和期望.
的分布列和期望.
相关知识点
推荐套卷
某电视台有A、B两种智力闯关游戏,甲、乙、丙、丁四人参加,其中甲乙两人各自独立进行游戏A,丙丁两人各自独立进行游戏B.已知甲、乙两人各自闯关成功的概率均为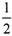 ,丙、丁两人各自闯关成功的概率均为
,丙、丁两人各自闯关成功的概率均为 .
.
(I )求游戏A被闯关成功的人数多于游戏B被闯关成功的人数的概率;
(II) 记游戏A、B被闯关成功的总人数为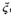 ,求
,求 的分布列和期望.
的分布列和期望.